强化学习基本概念
强化学习是一种试错方法,其目标是让软件智能体在特定环境中能够采取回报最大化的行为。强化学习在马尔可夫决策过程环境中主要使用的技术是动态规划(Dynamic Programming)。流行的强化学习方法包括自适应动态规划(ADP)、时间差分(TD)学习、状态-动作-回报-状态-动作(SARSA)算法、Q 学习、深度强化学习(DQN);其应用包括下棋类游戏、机器人控制和工作调度等。
举例来说,让我们考虑学习下象棋的问题。监督学习情况下的智能体(agent)需要被告知在每个所处的位置的正确动作,但是提供这种反馈很不现实。在没有教师反馈的情况下,智能体需要学习转换模型来控制自己的动作,也可能要学会预测对手的动作。但假如智能体得到的反馈不好也不坏,智能体将没有理由倾向于任何一种行动。当智能体下了一步好棋时,智能体需要知道这是一件好事,反之亦然。这种反馈称为奖励(reward)或强化(reinforcement)。在象棋这样的游戏中,智能体只有在游戏结束时才会收到奖励/强化。在其他环境中,奖励可能会更频繁。
强化学习的基本要素,我们对其分别进行定义:
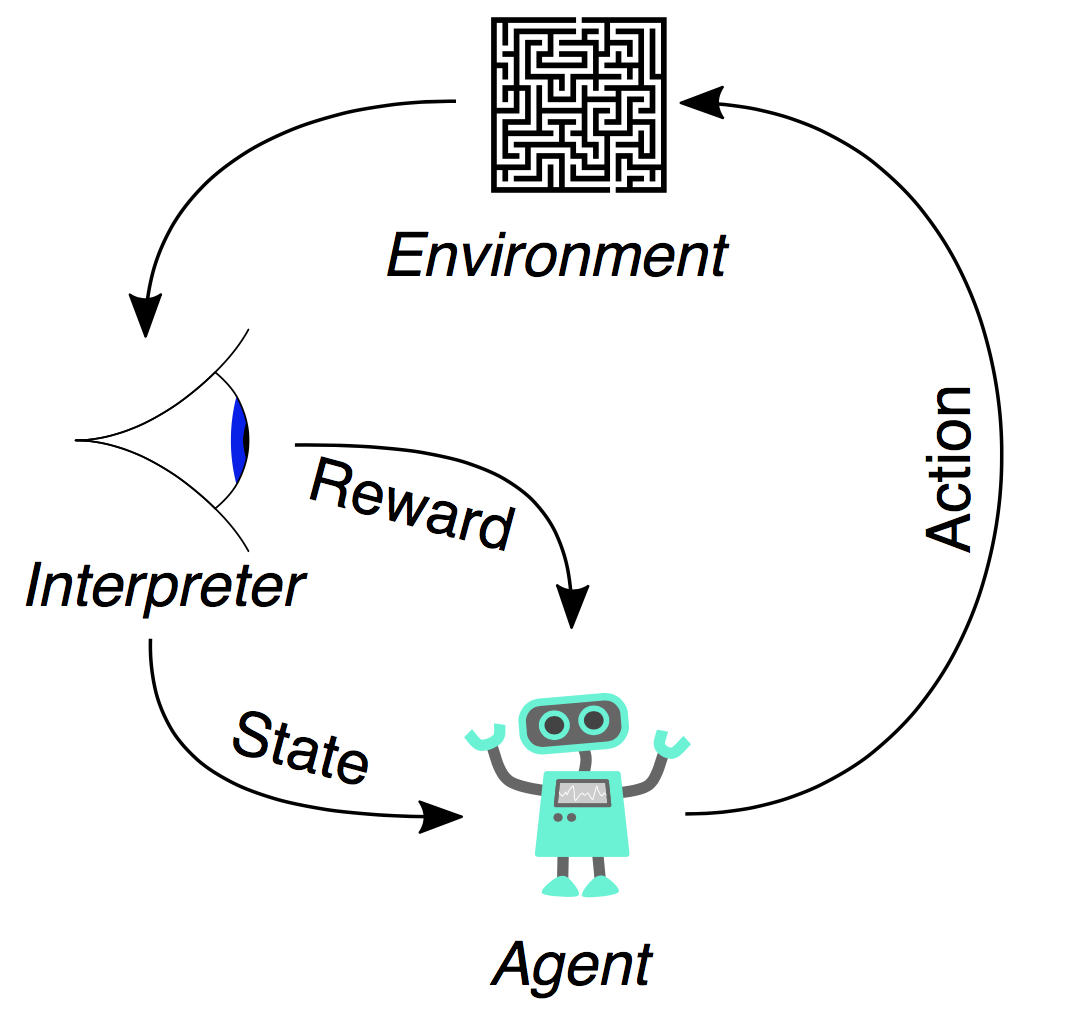
- 智能体(Agent):可以采取行动的智能个体;例如,可以完成投递的无人机,或者在视频游戏中朝目标行动的超级马里奥。强化学习算法就是一个智能体。而在现实生活中,那个智能体就是你。
- 行动(Action):A是智能体可以采取的行动的集合。一个行动(action)几乎是一目了然的,但是应该注意的是智能体是在从可能的行动列表中进行选择。在电子游戏中,这个行动列表可能包括向右奔跑或者向左奔跑,向高出处跳或者向低处跳,下蹲或者站住不动。在股市中,这个行动列表可能包括买入,卖出或者持有任何有价证券或者它们的变体。在处理空中飞行的无人机时,行动选项包含三维空间中的很多速度和加速度。
- 环境(Environment):指的就是智能体行走于其中的世界。这个环境将智能体当前的状态和行动作为输入,输出是智能体的奖励和下一步的状态。如果你是一个智能体,那么你所处的环境就是能够处理行动和决定你一系列行动的结果的物理规律和社会规则。
- 状态(State,S):一个状态就是智能体所处的具体即时状态;也就是说,一个具体的地方和时刻,这是一个具体的即时配置,它能够将智能体和其他重要的失事物关联起来,例如工具、敌人和或者奖励。它是由环境返回的当前形势。你是否曾在错误的时间出现在错误的地点?那无疑就是一个状态了。
- 奖励(Reward,R):奖励是我们衡量某个智能体的行动成败的反馈。例如,在视频游戏中,当马里奥碰到金币的时候,它就会赢得分数。面对任何既定的状态,智能体要以行动的形式向环境输出,然后环境会返回这个智能体的一个新状态(这个新状态会受到基于之前状态的行动的影响)和奖励(如果有任何奖励的话)。奖励可能是即时的,也可能是迟滞的。它们可以有效地评估该智能体的行动。
所以,环境就是能够将当前状态下采取的动作转换成下一个状态和奖励的函数;智能体是将新的状态和奖励转换成下一个行动的函数。我们可以知悉智能体的函数,但是我们无法知悉环境的函数。环境是一个我们只能看到输入输出的黑盒子。强化学习相当于智能体在尝试逼近这个环境的函数,这样我们就能够向黑盒子环境发送最大化奖励的行动了。
当然,奖励并不是强化学习的专利。在马尔科夫决策过程(MDP)中最优策略的定义也涉及到奖励。 最佳政策是最大化预期总回报的政策。 强化学习的任务是使用观察到的奖励来学习再当前环境中的最优(或接近最优)策略。 在这里我们假设智能体没有任何先验知识, 想象一下,玩一个你不知道的规则的新游戏; 经过一百次左右的动作之后,你的对手宣布:“你输了。”,这简直就是强化学习。
在许多复杂的领域,强化学习是实现高水平智能体的唯一可行方法。例如,在玩游戏时,人们很难提供对大量位置的准确和一致的评估——而若我们直接从示例中训练评估函数则这些信息是必须的——相反,在游戏中智能体可以在获胜或失败时被告知,并且可以使用这些信息来学习评估函数,使得该函数可以对任何给定位置的获胜概率进行合理准确的估计。
一般来说,强化学习的设计有三种:
- 基于效用的智能体(utility-based agent)学习状态的效用函数,并用它来选择最大化效用预期的操作;
- Q学习智能体(Q-learning agent)学习动作效用函数——又称Q函数——给出在给定状态下采取给定动作的预期效用;
- 反射智能体(reflex agent)学习从状态直接映射到操作的策略。
基于效用的智能体必须具有环境模型才能做出决策,因为它必须知道其行为将会导致什么状态。只有这样,它才能将效用函数应用于结果状态。另一方面,Q-learning智能体可以将预期效用与其可用选择进行比较,而不需要知道结果,因此它不需要环境模型。但由于在Q-learning中智能体不知道自己所处的环境,Q-learning智能体无法进行预测,这会严重限制他们的学习能力。
强化学习也可以分为被动学习和主动学习。被动学习中智能体的政策是固定的,任务是学习状态(或状态 – 行为配对)的效用,也可能涉及到学习环境模型。主动学习主要涉及的问题是探索:智能体必须尽可能多地体验其环境,以便学习如何表现。
[描述来源:Russell, S. J., & Norvig, P. (2010). Artificial Intelligence (A Modern Approach). ]
[描述来源:强化学习的基本概念与代码实现|机器之心 ]
发展历史
强化学习的发展历史并不长。强化学习的基础也才不过 50 多年历史。1953年,应用数学家Richard Bellman提出动态规划数学理论和方法,其中的贝尔曼条件(Bellman condition)是强化学习的基础之一。到20世纪50年代末,人们开始使用「最优控制(optimal control)」这一术语。1957年,Richard Bellman提出了马尔可夫决策过程,正确的理解马尔可夫决策过程对学习强化学习至关重要。到了60年代,「强化」和「强化学习」的概念开始在工程文献中出现。1963年,Andreae 开发出 STeLLA 系统,可以通过与环境交互进行试错学习;Donald Michie 描述了 MENACE——一种试错学习系统。这是早期简单的探索性研究。1975年,John Holland 基于选择原理阐述了自适应系统的一般理论。他的著作《自然系统和人工系统中的自适应(Adaptation in Natural and Artificial Systems)》的出版是人工智能领域的重要事件之一,除了对强化学习研究的影响,书中还普及了遗传算法,推动了搜索与优化的研究。
1977年,1977年,Paul Werbos介绍了一种求解自适应动态规划的方法,该方法后来被称为自适应校正设计(Adaptive Critic Designs)。自适应校正设计有许多同义词,包括近似动态规划(Approximate Dynamic Programming),渐近的动态规划(Asymptotic Dynamic Programming),自适应动态规划(Adaptive Dynamic Programming),启发式动态规划(Heuristic Dynamic Programming),神经动态规划(Neuro-Dynamic Programming)。奠定了后来的动态规划、强化学习的基础。Sutton于1988年介绍了一类专门用于预测的增量学习过程 – 也就是说,使用过去不完全知道的系统的经验来预测其未来行为。这即是时序差分法,对于大多数现实世界的预测问题,时间差分方法比当时的传统方法需要更少的内存和更少的峰值计算,并且它们可以产生更准确的预测。
1989年,Watkins在自己的博士论文(Learning from delayed rewards)中最早提出Q学习算法。1991年,Lovejoy 研究了部分可观测马尔可夫决策过程(POMDP)。1992年,Watkins和Dayan在机器学习的一个技术笔记(Technical note)给出了Q学习的收敛性证明,证明了当所有的状态都能重复访问时,Q函数最终会收敛到最优Q值。 1995年D. P. Bertsekas 和 J. N. Tsitsiklis讨论了一类用于不确定条件下的控制和顺序决策的动态规划方法。 这些方法具有处理长期以来由于状态空间较大或缺乏准确模型而难以处理的问题的潜力,他们将规划所基于的环境表述为马尔可夫决策过程,这即是目前深度学习领域流行的强化学习的雏形。
时间差分方法提出几年后,Tesauro基于Sutton的TD-Lambda算法开发了TD-Gammon,这是一个神经网络,通过与自己对抗并从结果中学习,他将TD-Gammon用于步步高游戏,该程序学会了在专业人类玩家的水平上玩步步高游戏,大大超越了以前的所有计算机程序。1994年,Rummery和Niranjan在一个名为“Modified Connectionist Q-Learning”(MCQ-L)的技术注释中提出了SARSA,这是一种学习马尔可夫决策过程策略的算法。1996年,Bertsekas和Tsitsiklis发表了Neuro-dynamic programming论文,详细介绍了神经动态规划算法的概况。1999年,为了能够进行可靠的位置估计,Thrun等人提出蒙特卡罗定位方法,使用概率方法解决机器人定位问题。他们的实证结果表明通过实验证明,所得到的方法能够在不知道其起始位置的情况下有效地定位移动机器人。与早期的基于网格的方法相比,它更快,更准确,内存更少。
2010年开始,强化学习技术(MDP 和动态规划)也被用于金融衍生品定价问题。2013年,来自DeepMind的Mnih等人在NIPS发表了Playing atari with deep reinforcement learning论文,论文中主体利用深度学习网络(CNNs)直接从高维度的感应器输入(sensory inputs)提取有效特征,然后利用Q-Learning学习主体的最优策略。这种结合深度学习的Q学习方法被称为深度Q学习(DQL)。2014年,Silver等人提出了确定性策略梯度算法,用于连续动作的强化学习。 确定性策略梯度具有特别吸引人的形式——它是行动价值函数的预期梯度。 这种简单的形式意味着对确定性策略梯度的估计可以比对通常的随机策略梯度估计更有效。2016年,Van Hasselt, H., Guez, A.提出了使用双Q-learning的深度强化学习。2017年10月,DeepMind发布最新强化版的AlphaGo Zero,这是一个无需用到人类专业棋谱的版本,比之前的版本都强大。通过自我对弈,AlphaGo Zero经过三天的学习就超越了AlphaGo Lee版本的水平,21天后达到AlphaGo Maseter的实力,40天内超越之前所有版本。2017年12月,DeepMind发布AlphaZero论文,进阶版的AlphaZero算法将围棋领域扩展到国际象棋、日本象棋领域,且无需人类专业知识就能击败各自领域的世界冠军。在 AAAI 2018 接收论文列表中,来自阿尔伯塔大学强化学习和人工智能实验室 Sutton 等研究者的一篇论文提出一种新的多步动作价值算法 Q(σ),该算法结合已有的时序差分算法,可带来更好性能。5月,DeepMind 在 Nature Neuroscience 发表新论文,该研究中他们根据神经科学中的多巴胺学习模型的扩展,强调了多巴胺在大脑最重要的智能区域即前额叶皮质发挥的整体作用,并据此提出了一种新型的元强化学习算法。
根据谷歌趋势上的数据来看,人们对强化学习的兴趣下降过一段时间。在深度学习的发展以及 AlphaGo 等成功应用的推动下,人们的兴趣最近又重回高位。因此,在强化学习经过了几十年的实验室研究和工程阶段之后,我们认为应该将其划入应用阶段。此外,也有很多机器人公司已经开始使用强化学习来训练商用机器人。
主要事件
| 年份 | 事件 | 相关论文/Reference |
| 1953 | Richard Bellman提出贝尔曼条件(Bellman condition),这是强化学习的基础之一 | Bellman, R. (1953). An introduction to the theory of dynamic programming.Rand Corporation Santa Monica Calif. |
| 1956/1957 | Bellman 介绍了动态规划和马尔可夫决策过程(MDP)的概念 | Bellman, R. (1957). A Markovian decision process. Journal of Mathematics and Mechanics, 679-684. |
| 1963 | Andreae 开发出 STeLLA 系统(通过与环境交互进行试错学习);Donald Michie 描述了 MENACE (一种试错学习系统) | Andreae, J. (1963). STELLA: A Scheme for a Learning Machine. |
| 1975 | John Holland基于选择原理阐述了自适应系统的一般理论 | Holland, J. H. (1992).Adaptation in Natural and Artificial Systems: An Introductory Analysis with Applications to Biology, Control and Artificial Intelligence.MIT Press. |
| 1977 | Werbos 提出自适应动态规划(ADP) | Werbos, P. (1977). Advanced forecasting methods for global crisis warning and models of intelligence. General System Yearbook, 25-38. |
| 1988 | R.S.Sutton 首次使用时间差分学习(TD 算法诞生) | Sutton, R. (1988). Learning to predict by the methods of temporal differences.Machine Learning. 3 (1): 9–44. |
| 1989 | Watkins提出了Q学习 | Watkins, C. J. C. H. (1989). Learning from delayed rewards (Doctoral dissertation, King’s College, Cambridge). |
| 1991 | Lovejoy 研究了部分可观测马尔可夫决策过程(POMDP) | Lovejoy, W. S. (1991).A survey of algorithmic methods for partially observed Markov decision processes.Annals of Operations Research. 28(1):47–65. |
| 1994 | Tesauro et al.将强化学习和神经网络结合到了一起 | Tesauro, G. (1995).Temporal Difference Learning and TD-Gammon.Communications of the ACM. 38 (3). |
| 1994 | Rummery提出SARSA | Rummery, G. A., & Niranjan, M. (1994). On-line Q-learning using connectionist systems (Vol. 37). University of Cambridge, Department of Engineering. |
| 1996 | Bertsekas提出神经动态规划(Neuro-Dynamic Programming) | Bertsekas, Dimitri P., and John N. Tsitsiklis. “Neuro-dynamic programming: an overview.” Decision and Control, 1995., Proceedings of the 34th IEEE Conference on. Vol. 1. IEEE, 1995. |
| 1999 | Thrun等人提出蒙特卡罗定位方法 | Dellaert, F.; Fox, D.; Burgard, W. and Thrun, S. (1999). Monte Carlo localization for mobile robots.Proceedings 1999 IEEE International Conference on Robotics and Automation. 2: 1322-1328. |
| 2013 | Mnih et al.提出深度Q学习(DQN) | Mnih, V., Kavukcuoglu, K., Silver, D., Graves, A., Antonoglou, I., Wierstra, D., & Riedmiller, M. (2013). Playing atari with deep reinforcement learning. arXiv preprint arXiv:1312.5602. |
| 2014 | Silver提出确定性策略梯度学习(Policy Gradient Learning) | Silver, D.; Lever, G.; Heess, N.; Degris, T.; Wierstra, D. et al .(2014). Deterministic Policy Gradient Algorithms. ICML. |
| 2016 | AlphaGo(Silver et al.)成为深度强化学习应用的著名案例 | Silver, D., Huang, A., Maddison, C. J., Guez, A., Sifre, L., Van Den Driessche, G., … & Dieleman, S. (2016). Mastering the game of Go with deep neural networks and tree search. Nature, 529(7587), 484-489. |
| 2016 | Van Hasselt, H., Guez, A.使用双Q-learning的深度强化学习 | Van Hasselt, H., Guez, A., & Silver, D. (2016, February). Deep Reinforcement Learning with Double Q-Learning. In AAAI (Vol. 16, pp. 2094-2100). |
| 2017 | DeepMind公司发布AlphaZero论文,进阶版的AlphaZero算法将围棋领域扩展到国际象棋、日本象棋领域,且无需人类专业知识就能击败各自领域的世界冠军 | Silver, D., Hubert, T., Schrittwieser, J., Antonoglou, I., Lai, M., Guez, A., … & Lillicrap, T. (2017). Mastering Chess and Shogi by Self-Play with a General Reinforcement Learning Algorithm. arXiv preprint arXiv:1712.01815. |
| 2017 | Sutton和Barto等学者提出了Q(σ)算法 | Asis, K. D. et al.Multi-step Reinforcement Learning: A Unifying Algorithm.arXiv:1703.01327. |
| 2018 | DeepMind在Nature Neuroscience发表新论文提出了一种新型的元强化学习算法 | Wang, J. X. et al. (2018). Prefrontal cortex as a meta-reinforcement learning system. Nature Neuroscience. |
发展分析
瓶颈
- 强化学习的训练通常在自有规则的虚拟环境中进行,而现实世界往往要复杂得多。
- 训练速度慢,而且往往需要大量样本作为基础。
- 强化学习的商业应用仍然很有限,而且前景不明,类似于神经网络模型发展的早期阶段。
- 目前流行的深度强化学习奖励函数设计困难、采样效率底下(sample inefficiency),即便最合理的奖励也不能避免局部最优,因而训练难度大。
未来发展方向
- 需要更少数据的「一次性学习(one shot learning)」以及可以独立学习智能体动作的「离策略学习(off policy learning)」的改进和完善值得期待。
- 强化学习与深度学习等其它智能方法的结合会有一个光明的未来,可以将更多智能带进游戏、驾驶和机器人等不同应用中。
- 目前有基于模型的深度强化学习,试图学习环境的动态模型,能够大大提高采样效率(sample efficiency),从而提高学习效率。
Contributor: Yuanyuan Li, Mos Zhang
原文:https://www.jiqizhixin.com/graph/technologies/ee1a8f69-3170-4ddf-b2b6-47d91c844425
既然来了,说些什么?