深入探讨：为什么要做特征归一化/标准化？

本文解读了一项数据预处理中的重要技术——特征归一化，提出并解答了5个相关问题，同时分析了相关方法和适用场景。

写在前面

Feature scaling，常见的提法有“特征归一化”、“标准化”，是数据预处理中的重要技术，有时甚至决定了算法能不能work以及work得好不好。谈到feature scaling的必要性，最常用的2个例子可能是：

• 特征间的单位（尺度）可能不同，比如身高和体重，比如摄氏度和华氏度，比如房屋面积和房间数，一个特征的变化范围可能是[1000, 10000]，另一个特征的变化范围可能是[−0.1,0.2]，在进行距离有关的计算时，单位的不同会导致计算结果的不同，尺度大的特征会起决定性作用，而尺度小的特征其作用可能会被忽略，为了消除特征间单位和尺度差异的影响，以对每维特征同等看待，需要对特征进行归一化。
• 原始特征下，因尺度差异，其损失函数的等高线图可能是椭圆形，梯度方向垂直于等高线，下降会走zigzag路线，而不是指向local minimum。通过对特征进行zero-mean and unit-variance变换后，其损失函数的等高线图更接近圆形，梯度下降的方向震荡更小，收敛更快，如下图所示，图片来自Andrew Ng。

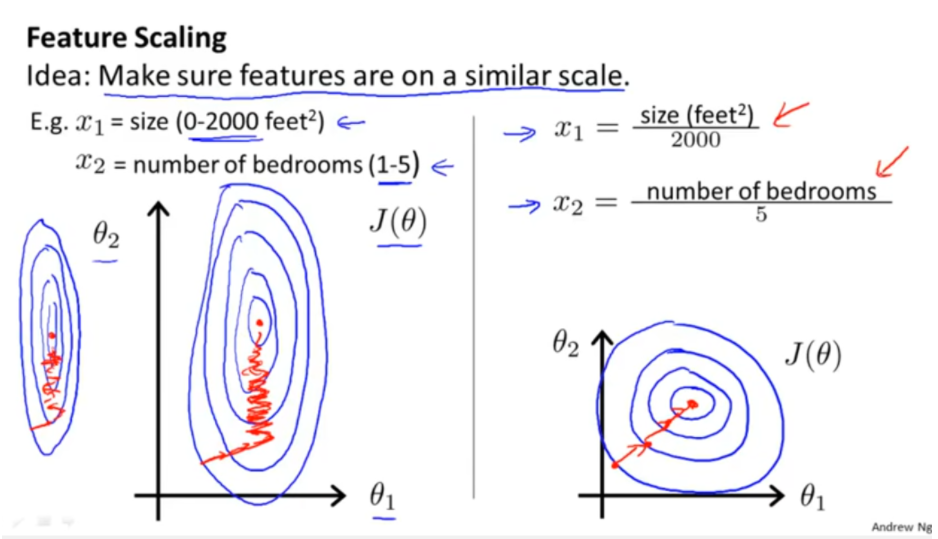
对于feature scaling中最常使用的Standardization，似乎“无脑上”就行了，本文想多探究一些为什么，

• 常用的feature scaling方法都有哪些？
• 什么情况下该使用什么feature scaling方法？有没有一些指导思想？
• 所有的机器学习算法都需要feature scaling吗？有没有例外？
• 损失函数的等高线图都是椭圆或同心圆吗？能用椭圆和圆来简单解释feature scaling的作用吗？
• 如果损失函数的等高线图很复杂，feature scaling还有其他直观解释吗？

根据查阅到的资料，本文将尝试回答上面的问题。但笔者能力有限，空有困惑，能讲到哪算哪吧（微笑）。

常用feature scaling方法

在问为什么前，先看是什么。

给定数据集，令特征向量为x，维数为D，样本数量为R，可构成D×R的矩阵，一列为一个样本，一行为一维特征，如下图所示，图片来自Hung-yi Lee pdf-Gradient Descent：

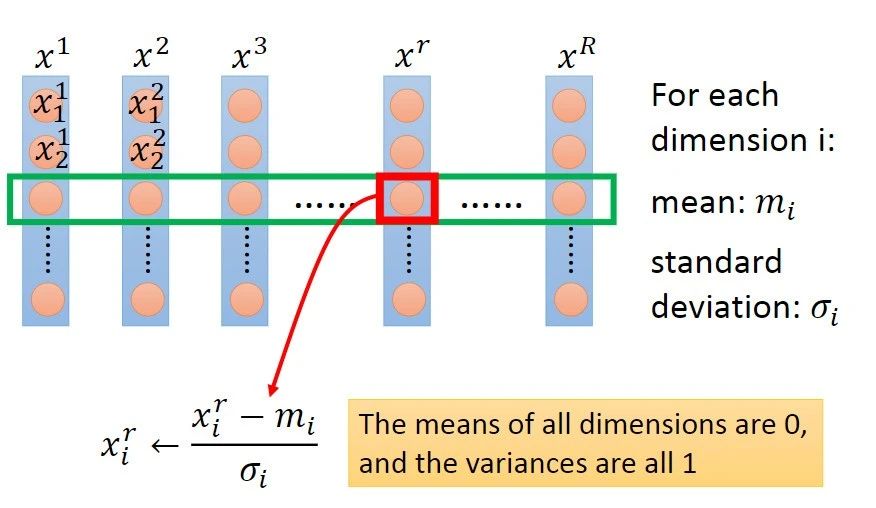
feature scaling的方法可以分成2类，逐行进行和逐列进行。逐行是对每一维特征操作，逐列是对每个样本操作，上图为逐行操作中特征标准化的示例。

具体地，常用feature scaling方法如下，来自wiki，

• Rescaling (min-max normalization、range scaling)：

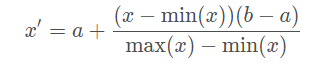
将每一维特征线性映射到目标范围[a,b]，即将最小值映射为a，最大值映射为b，常用目标范围为[0,1]和[−1,1]，特别地，映射到[0,1]计算方式为：

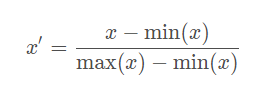
• Mean normalization：

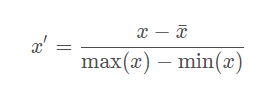
将均值映射为0，同时用最大值最小值的差对特征进行归一化，一种更常见的做法是用标准差进行归一化，如下。

• Standardization (Z-score Normalization)：

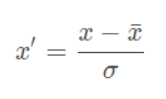
每维特征0均值1方差（zero-mean and unit-variance）。

• Scaling to unit length：

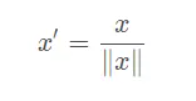
将每个样本的特征向量除以其长度，即对样本特征向量的长度进行归一化，长度的度量常使用的是L2 norm（欧氏距离），有时也会采用L1 norm，不同度量方式的一种对比可以参见论文“CVPR2005-Histograms of Oriented Gradients for Human Detection”。

上述4种feature scaling方式，前3种为逐行操作，最后1种为逐列操作。

容易让人困惑的一点是指代混淆，Standardization指代比较清晰，但是单说Normalization有时会指代min-max normalization，有时会指代Standardization，有时会指代Scaling to unit length。

计算方式上对比分析

前3种feature scaling的计算方式为减一个统计量再除以一个统计量，最后1种为除以向量自身的长度。

• 减一个统计量可以看成选哪个值作为原点，是最小值还是均值，并将整个数据集平移到这个新的原点位置。如果特征间偏置不同对后续过程有负面影响，则该操作是有益的，可以看成是某种偏置无关操作；如果原始特征值有特殊意义，比如稀疏性，该操作可能会破坏其稀疏性。
• 除以一个统计量可以看成在坐标轴方向上对特征进行缩放，用于降低特征尺度的影响，可以看成是某种尺度无关操作。缩放可以使用最大值最小值间的跨度，也可以使用标准差（到中心点的平均距离），前者对outliers敏感，outliers对后者影响与outliers数量和数据集大小有关，outliers越少数据集越大影响越小。
• 除以长度相当于把长度归一化，把所有样本映射到单位球上，可以看成是某种长度无关操作，比如，词频特征要移除文章长度的影响，图像处理中某些特征要移除光照强度的影响，以及方便计算余弦距离或内积相似度等。

稀疏数据、outliers相关的更多数据预处理内容可以参见scikit learn-5.3. Preprocessing data。

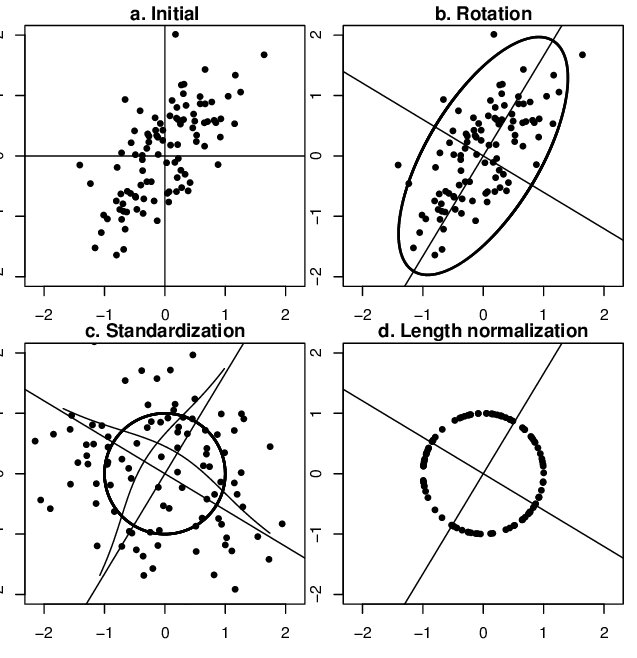
从几何上观察上述方法的作用，图片来自CS231n-Neural Networks Part 2: Setting up the Data and the Loss，zero-mean将数据集平移到原点，unit-variance使每维特征上的跨度相当，图中可以明显看出两维特征间存在线性相关性，Standardization操作并没有消除这种相关性。

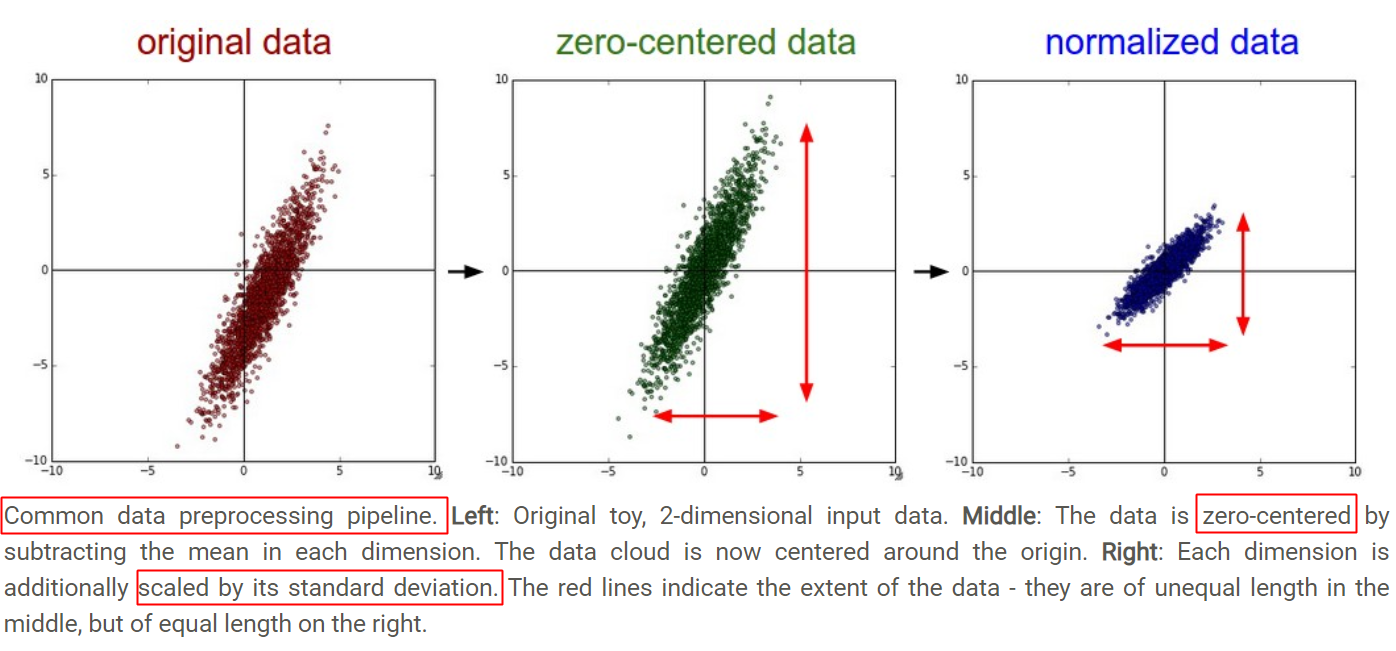
可通过PCA方法移除线性相关性（decorrelation），即引入旋转，找到新的坐标轴方向，在新坐标轴方向上用“标准差”进行缩放，如下图所示，图片来自链接，图中同时描述了unit length的作用——将所有样本映射到单位球上。

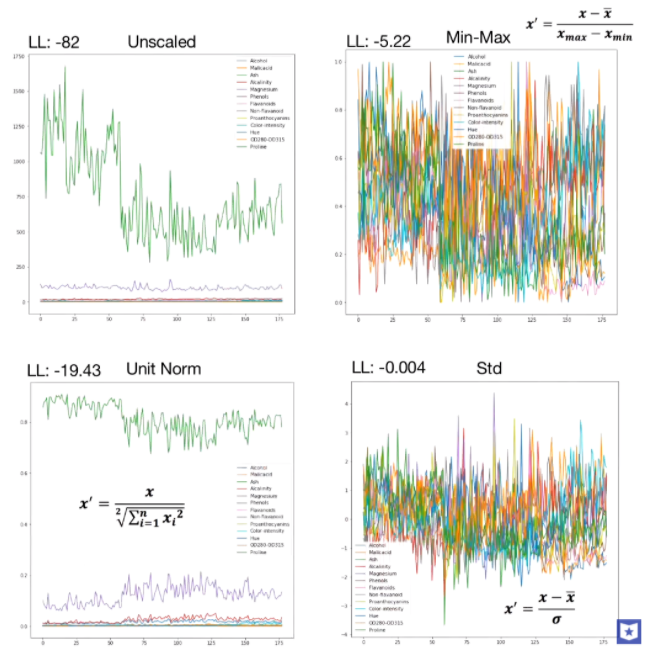
当特征维数更多时，对比如下，图片来自youtube，

总的来说，归一化/标准化的目的是为了获得某种“无关性”——偏置无关、尺度无关、长度无关……当归一化/标准化方法背后的物理意义和几何含义与当前问题的需要相契合时，其对解决该问题就有正向作用，反之，就会起反作用。所以，“何时选择何种方法”取决于待解决的问题，即problem-dependent。

feature scaling 是否需要

下图来自data school-Comparing supervised learning algorithms，对比了几个监督学习算法，最右侧两列为是否需要feature scaling。

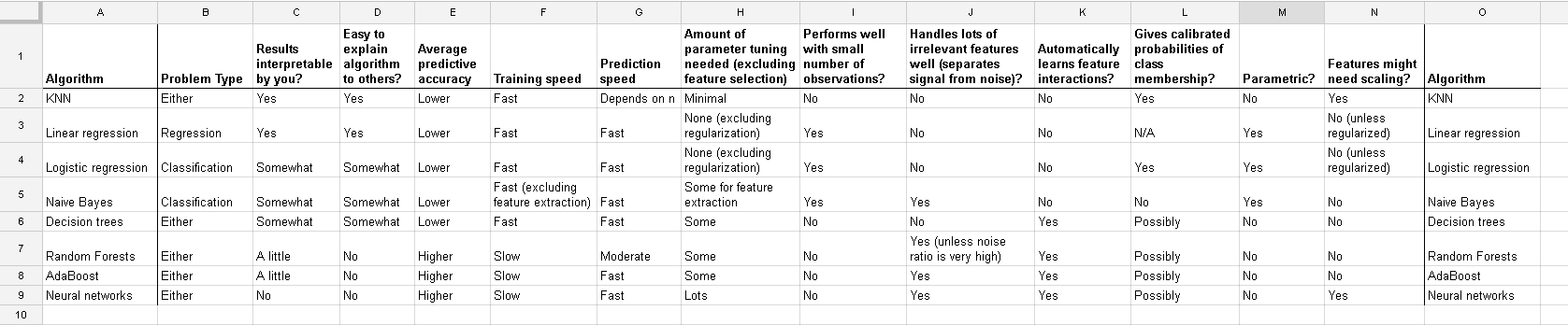
下面具体分析一下。

什么时候需要feature scaling？

• 涉及或隐含距离计算的算法，比如K-means、KNN、PCA、SVM等，一般需要feature scaling，因为：

zero-mean一般可以增加样本间余弦距离或者内积结果的差异，区分力更强，假设数据集集中分布在第一象限遥远的右上角，将其平移到原点处，可以想象样本间余弦距离的差异被放大了。在模版匹配中，zero-mean可以明显提高响应结果的区分度。

就欧式距离而言，增大某个特征的尺度，相当于增加了其在距离计算中的权重，如果有明确的先验知识表明某个特征很重要，那么适当增加其权重可能有正向效果，但如果没有这样的先验，或者目的就是想知道哪些特征更重要，那么就需要先feature scaling，对各维特征等而视之。

增大尺度的同时也增大了该特征维度上的方差，PCA算法倾向于关注方差较大的特征所在的坐标轴方向，其他特征可能会被忽视，因此，在PCA前做Standardization效果可能更好，如下图所示，图片来自scikit learn-Importance of Feature Scaling，

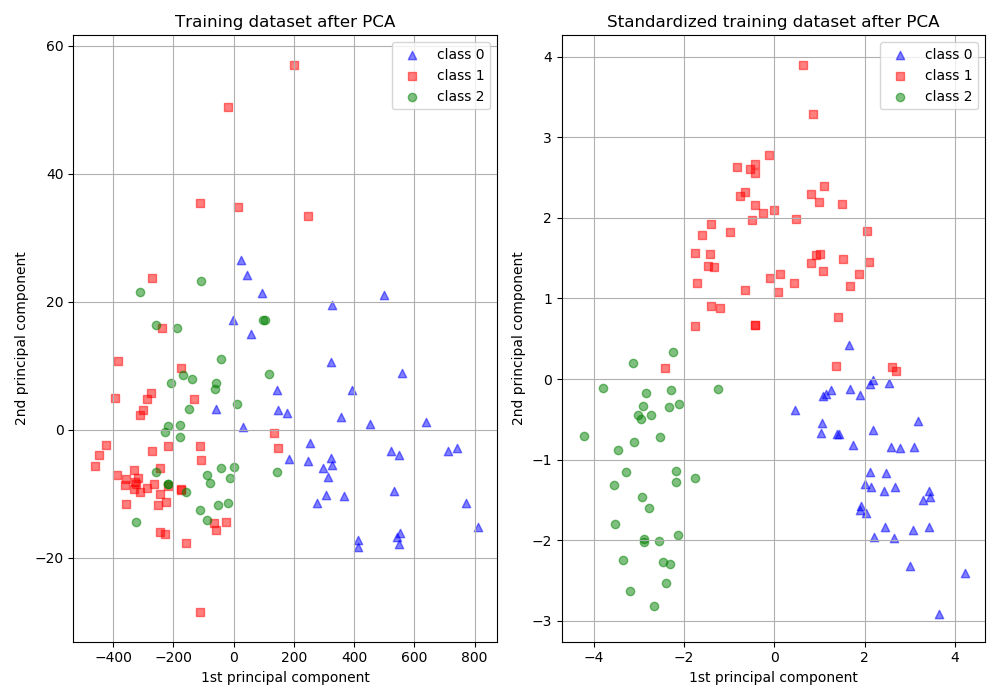
• 损失函数中含有正则项时，一般需要feature scaling：对于线性模型y=wx+b而言，x的任何线性变换（平移、放缩），都可以被w和b“吸收”掉，理论上，不会影响模型的拟合能力。但是，如果损失函数中含有正则项，如λ∣∣w∣∣^2，λ为超参数，其对w的每一个参数施加同样的惩罚，但对于某一维特征xi而言，其scale越大，系数wi越小，其在正则项中的比重就会变小，相当于对wi惩罚变小，即损失函数会相对忽视那些scale增大的特征，这并不合理，所以需要feature scaling，使损失函数平等看待每一维特征。
• 梯度下降算法，需要feature scaling。梯度下降的参数更新公式如下，

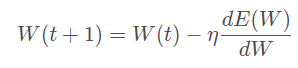
E(W)为损失函数，收敛速度取决于：参数的初始位置到local minima的距离，以及学习率η的大小。一维情况下，在local minima附近，不同学习率对梯度下降的影响如下图所示：

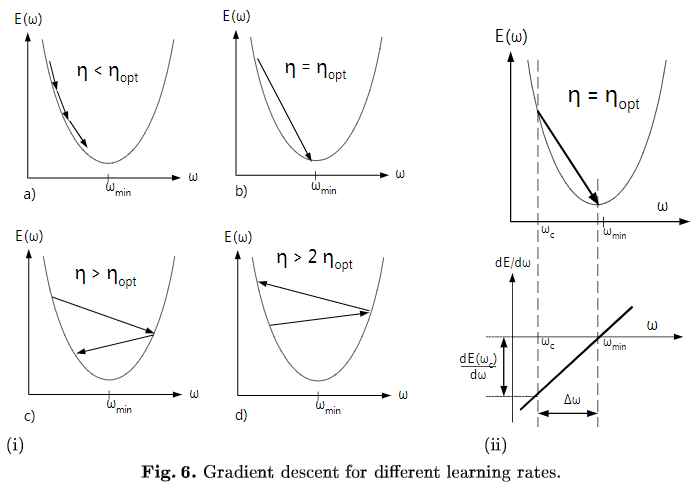
多维情况下可以分解成多个上图，每个维度上分别下降，参数W为向量，但学习率只有1个，即所有参数维度共用同一个学习率（暂不考虑为每个维度都分配单独学习率的算法）。收敛意味着在每个参数维度上都取得极小值，每个参数维度上的偏导数都为0，但是每个参数维度上的下降速度是不同的，为了每个维度上都能收敛，学习率应取所有维度在当前位置合适步长中最小的那个。下面讨论feature scaling对gradient descent的作用，

• zero center与参数初始化相配合，缩短初始参数位置与local minimum间的距离，加快收敛。模型的最终参数是未知的，所以一般随机初始化，比如从0均值的均匀分布或高斯分布中采样得到，对线性模型而言，其分界面初始位置大致在原点附近，bias经常初始化为0，则分界面直接通过原点。同时，为了收敛，学习率不会很大。而每个数据集的特征分布是不一样的，如果其分布集中且距离原点较远，比如位于第一象限遥远的右上角，分界面可能需要花费很多步骤才能“爬到”数据集所在的位置。所以，无论什么数据集，先平移到原点，再配合参数初始化，可以保证分界面一定会穿过数据集。此外，outliers常分布在数据集的外围，与分界面从外部向内挪动相比，从中心区域开始挪动可能受outliers的影响更小。
• 对于采用均方误差损失LMS的线性模型，损失函数恰为二阶，如下图所示

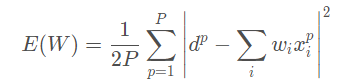不同方向上的下降速度变化不同（二阶导不同，曲率不同），恰由输入的协方差矩阵决定，通过scaling改变了损失函数的形状，减小不同方向上的曲率差异。将每个维度上的下降分解来看，给定一个下降步长，如果不够小，有的维度下降的多，有的下降的少，有的还可能在上升，损失函数的整体表现可能是上升也可能是下降，就会不稳定。scaling后不同方向上的曲率相对更接近，更容易选择到合适的学习率，使下降过程相对更稳定。

• 另有从Hessian矩阵特征值以及condition number角度的理解，详见Lecun paper-Efficient BackProp中的Convergence of Gradient Descent一节，有清晰的数学描述，同时还介绍了白化的作用——解除特征间的线性相关性，使每个维度上的梯度下降可独立看待。
• 文章开篇的椭圆形和圆形等高线图，仅在采用均方误差的线性模型上适用，其他损失函数或更复杂的模型，如深度神经网络，损失函数的error surface可能很复杂，并不能简单地用椭圆和圆来刻画，所以用它来解释feature scaling对所有损失函数的梯度下降的作用，似乎过于简化，见Hinton vedio-3.2 The error surface for a linear neuron。
• 对于损失函数不是均方误差的情况，只要权重w与输入特征x间是相乘关系，损失函数对w的偏导必然含有因子x，w的梯度下降速度就会受到特征x尺度的影响。理论上为每个参数都设置上自适应的学习率，可以吸收掉x尺度的影响，但在实践中出于计算量的考虑，往往还是所有参数共用一个学习率，此时x尺度不同可能会导致不同方向上的下降速度悬殊较大，学习率不容易选择，下降过程也可能不稳定，通过scaling可对不同方向上的下降速度有所控制，使下降过程相对更稳定。
• 对于传统的神经网络，对输入做feature scaling也很重要，因为采用sigmoid等有饱和区的激活函数，如果输入分布范围很广，参数初始化时没有适配好，很容易直接陷入饱和区，导致梯度消失，所以，需要对输入做Standardization或映射到[0,1]、[−1,1]，配合精心设计的参数初始化方法，对值域进行控制。但自从有了Batch Normalization，每次线性变换改变特征分布后，都会重新进行Normalization，似乎可以不太需要对网络的输入进行feature scaling了？但习惯上还是会做feature scaling。

什么时候不需要Feature Scaling？

与距离计算无关的概率模型，不需要feature scaling，比如Naive Bayes；

与距离计算无关的基于树的模型，不需要feature scaling，比如决策树、随机森林等，树中节点的选择只关注当前特征在哪里切分对分类更好，即只在意特征内部的相对大小，而与特征间的相对大小无关。

小结

这篇文章写得十分艰难，一开始以为蛮简单直接，但随着探索的深入，冒出的问号越来越多，打破了很多原来的“理所当然”，所以，在写的过程中不停地做加法，很多地方想解释得尽量直观，又不想照搬太多公式，但自己的理解又不够深刻，导致现在叙述这么冗长，希望以后在写文时能更专注更精炼。

原文：https://mp.weixin.qq.com/s/0wMEC-W-ctzu8iDYsBegAg