AI产品之路:机器学习
2017年可以说是人工智能爆发的一年,传统互联网红利消失,熟知的大厂BAT都在人工智能上布局,作为一名互联网PM,深知技术的变革必然带来新机会。可对大多数互联网PM而言,面对ML(机器学习)、DL(深度学习)、NLP(自然语言处理)以及的各种概念以及底层所需的各种数学知识,不懂技术似乎让人望而却步了。
可事实并非全然如此,AI是手段,最终的目的也是要找到现实中可以落地和商业化的场景,去实现他的价值,虽然目前来看仍然是技术主导。不过可以确信的一点是,要进入这个领域,对底层知识和技术的要求是必然要高于互联网PM的水平。
本人目前是一名互联网PM,刚好上学得是相关专业,有点数学底子,也层自己撸过代码设计实现“基于BP前馈神经网络的图像识别”,打算进入未来进入AI领域,最近开始重新学习并搭建AI的知识框架,希望能分享出来大家一起来了解AI这个看起来“高大上”的东西。
首先,按照李笑来老师和罗胖的说法,学一个领域的知识,就是两件事(1)找概念(2)搭框架。特别是对于很多对概念都不了解的同学,一定要有个“知识地图”,如下:
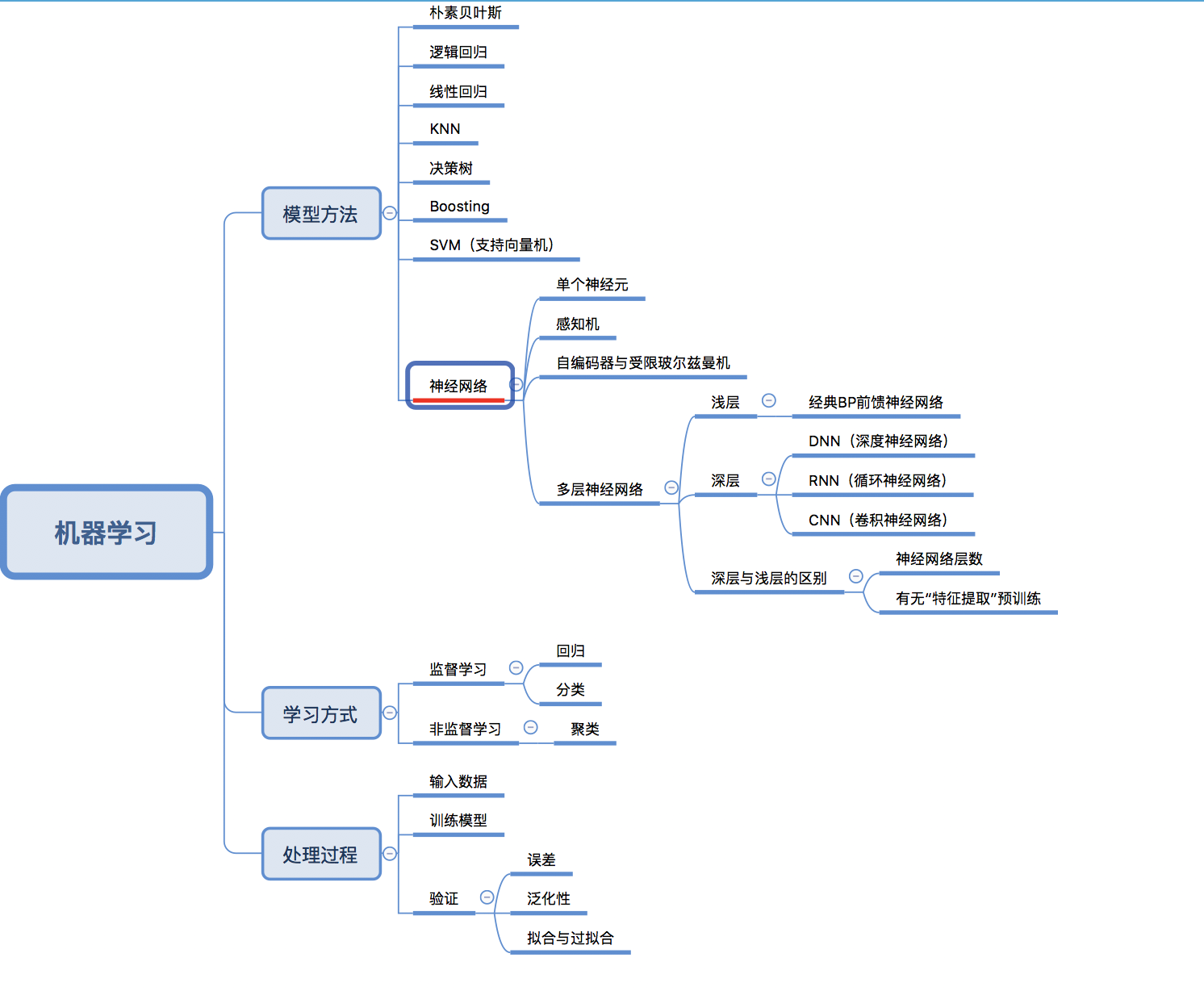
看到这个脑图,一些童鞋经常混淆的问题就明白了
- 机器学习是什么
- 深度学习是什么
- 机器学习与深度学习的区别是什么
- 机器学习监督学习方式的“回归思想”
下面我们一一来说
1.机器学习
概念定义(个人理解):通过大量已知数据(可能被标注,也可能无标注)去训练算法模型,总结出某种数据之间的映射关系(即规律),最终可以对未知数据实现智能处理(分类、识别、预测等)
举个例子,比如我这里有大量苹果和桃子的图片,并且每张图片都打上对应的种类标签,然后把这些图片喂给模型,让模型不断学习优化。训练结束后,我们又找一些没有打标签的苹果和桃子图片扔给这个模型,让他自己去做分类识别是苹果还是桃子,这就是一个完整的机器学习过程(有监督)。而所谓的“映射关系”,即“苹果图片”对应“苹果标签”,“桃子图片”对应“桃子标签”
2.基本概念
(1)学习方式
学习方式分为有监督学习和无监督学习,有监督学习即我们会再把数据给模型训练之前,进行人工的预先处理,打标签(学名:特征提取)。监督学习又分为回归与分类。
而无监督学习,就是无需通过人为的预先处理,直接把数据给算法,无监督学习对应的方法为“聚类”
(2)学习过程
- 训练集(训练样本):我们在训练算法模型时给他的数据
- 验证集:用训练样本训练好以后,我们还要用训练样本之外的数据,去检验这个算法模型的实际效果
- 误差:如何检验效果呢?在ML/DL里,就是通过“误差”的大小去判断(至于具体怎么计算,下一篇会讲到)
- 欠拟合:模型不能在训练集上获得足够低的误差
- 过拟合:训练误差与测试误差(在验证集的误差)差距过大,那么这个模型就不是好模型,因为只能用在训练样本上….而对其以外的数据都没有好的效果
- 泛化性:训练好的模型在其他数据上的使用情况,如果效果也很好,那就是泛化性好
那么问题来了,怎样才算合适的拟合呢?
其实在整个过程中,随着时间推移,算法的不断优化,在训练样本和测试样本的误差都在不断下降;但如果学习时间过程,训练集的误差持续下降,而验证集的误差却开始上升了。原因是模型为了在训练集上效果更好!已经开始学习训练集上的噪音和不需要的细节了。所以要找到合适的“拟合”,最好是找到训练误差还在下降,而测试误差刚好开始上升的那个“点”
3.机器学习与深度学习的区别
很多不知道的人,可能仅仅知道他们是包含关系,深度学习属于机器学习,但其实远远不止如此…..(这样太模糊了),从脑图可以看出,其实机器学习在方法上可以有很多种,比如:逻辑回归、决策树、朴素贝叶斯、线性回归、SVM支持向量机等,他们都属于机器学习,而我们也看到,最下面有一个“神经网络”,他们的等级与上面列举是属于一类的。
而神经网络这概念,可以分为“浅层神经网络”与“深层神经网络”
“浅层神经网络”中最经典的一个网络也就是“BP前馈神经网络”
“深层神经网络”,大概可以理解为我们所谓的“深度学习”(Deep Learning),而深层神经网络,下面又分为很多网络结构,如DNN、CNN、RNN
但这里要注意区分的是,深浅的区别不仅仅是“网络层数”的区别,更重要的是,“深度学习”(深层神经网络)较其他所有机器学习最厉害的一点:
他可以进行数据的特征提取“预处理”(省去了数据人工标注的大麻烦,同时可以对更多维和复杂的特征进行向量的提取和空间向量的转换,方便后续处理),而这也是他为什么要很多层的原因,因为其中多出来的网络层数,都是要用来进行数据特征提取预处理的
相信到一步,结合上面的脑图,我们就能分清“机器学习”与“深度学习”的真正区别了,不是简单的包含关系。
4.回归
个人觉得回归作为了解机器学习过程,是一个很好的入门了解。
所谓“回归”,看起来很深奥,其实并不是这样。我举个栗子:
y=2x这个一元函数,假设我们现在不知道他的斜率w=2,而我给你5数据y=2,4,6,8,10,对应的x分别为1,2,3,4,5。你是不是会自动假设,那他们之间是2倍的对应关系?没错!你“自动假设他们有某种对应关系”的这个过程,就叫“回归”;而你假设他们的关系是“2倍”,这就是“线性回归”了。
所以回归的定义(个人理解):我们看到大量事实或数据中,假设他们之间存在着某种对应关系。而机器学习中的回归(监督学习)要做的就是:尝试去让计算机找到大量数据之间这样的对应关系,那怎么找呢?
我们先假设一个关系吧:y=wx+b ,其中 w为权值、b为偏置,w为1Xn矩阵向量,x为nX1的矩阵向量(这几个概念就不做数学解释了,而为什么x不是实数而是矩阵,那是因为我们在现实世界的数据中,可能有N多个维度….而不仅仅是一维就可以描述这个数据特征的)
现在我要评判一个橘子的“好坏程度”,y代表“好坏程度”,而且都是打过标签的。x为一个三维矩阵向量分别代表【大小、颜色、形状】。那么代入公式:
y=w1X大小+w2X颜色+w3X形状+b (这里先假设b为0吧)
那么现在的任务就是分别找到合适的w1,w2,w3的值来准确描述橘子的“好坏程度”与“大小、颜色、形状”的关系。那么怎样确定是否合适呢?
通过“损失函数”Loss来定义(这里数学公式就不列了),Loss的含义就是把样本中所有x都代入“假设公式”wx+b中(这时候w与b的值几乎肯定是不准确的),然后得到值与真实的y值做比较的差值,就是损失函数Loss。那么Loss越小,说明这时候的w与b的值越接近真实的“线性关系”。所以我们最终机器学习的目的,就是求解出让Loss越小(当然无限接近于0最好)的对应的w与b的值,求出来之后,也就是机器学习模型“训练结束”!之后就是用验证集去验证是否会过拟合,来检验模型的泛化能力
当然这里要做几点说明了:
(1)这只是最为最为简单的一个机器学习栗子说明,着重了解一下机器学习中回归的基本思想
(2)这里我们并没有说怎么去寻找让Loss最小(或符合条件)的对应w与b的映射关系,后面我在分享“BP前馈神经网络的梯度下降时”会简单介绍这个求解基本思想过程
(3)如果你分析的数据本身是非线性关系,而你假设他们是线性关系并用对应的模型去训练,那么结果一定是“欠拟合”的(所以对于欠拟合的一另一个表达:你的想法不符合这个世界的现实…)
上篇文章里,主要分享了关于机器学习、深度学习的基本概念和他们之间的区别,最后介绍了有监督学习方式中的回归。其实我在最后留下一点小问题,那就是如果数据不是线性关系的话,怎么回归?这篇文章就会回答这个问题,主要分享监督学习和非监督学习中的三大类:
- 监督学习方式下,回归中的“非线性回归”
- 监督学习方式下的“分类”
- 非监督学习方式的“聚类”
- 关于机器学习的复盘
1.非线性回归
直逼主题,上篇我们假定的数据都是线性的,那么最后当然可以回归出y=wx+b这样的线性方程,可我们最终是想通过机器学习解决现实问题,而现实中的很多数据不可能单单是线性关系,如果强行使用,那么算法模型只能是欠拟合,误差非常大。
这里我们就着重说一下,回归中的非线性回归,而其中应用最多的就是“逻辑回归”。
先上公式:
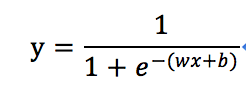
看到这个公式先别慌,其中你们注意(wx+b)是我们上篇已经熟悉的线性回归方程,把它想象成一个整体,带入到这个新公式中,代表着什么呢?下面我们看这个公式的函数图
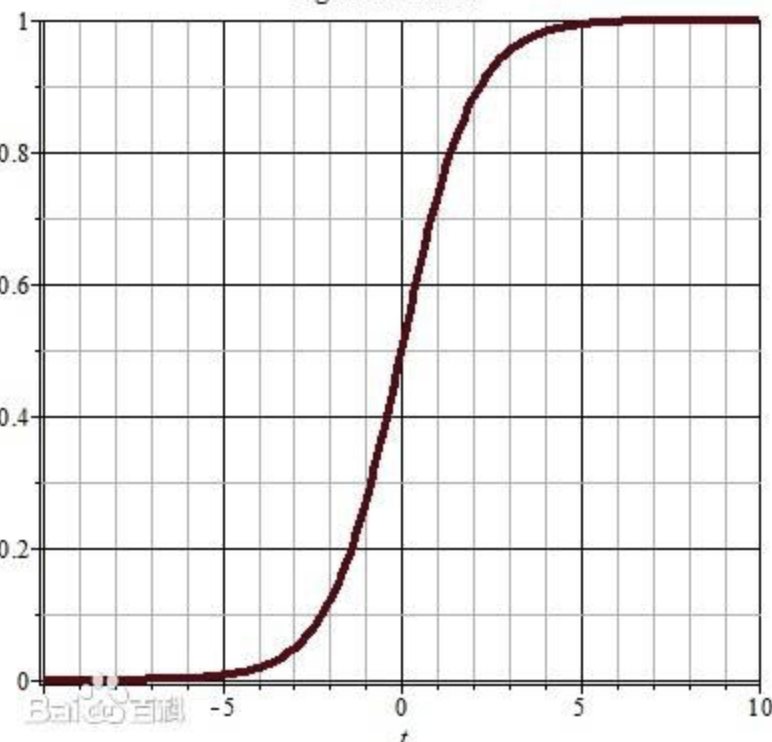
可以看到,在x可以取(-无穷小,+无穷大)的区间里,整个y值是的区间只能是【0,1】之间。具体的数学函数转换如果搞不明白完全没关系,只需要回忆一下上一篇中“线性回归”的思想,通过找到损失函数Loss最小的对应wx+b中对应的w与b的值。而这个逻辑回归函数的作用,在仅仅是把x多映射一次,即让输出的y值恒定落在【0,1】这个区间而已,其回归思想的本质并没有改变。
那么为什么要加入这个函数呢?其实是方便做概率判断:
因为这个函数会让x无论输入的是什么,最终输出的y肯定是0-1之间的值,那么越接近1,我们可以认为越接近“1”代表的特征,越接近0,我们认为越接近“0”代表的特征。而“0”与“1”具体要赋予什么意义,就看我们到底想通过机器学习去识别什么了。
2.监督学习–“分类”
先感性谈谈“分类”这个概念。就是我们希望有一台机器,可以帮助我们进行图像的分类识别。比如我这里有一堆混杂着“鱼”、“狗”和“猫”的图片,光靠人力完成是非常困难的,我想通把这些大量的数据输入给计算机,它很快就能完成而不需要耗费我很长时间去一个一个挑选。但我们知道计算机天生不具备这样的功能,就可以通过机器学习中的“分类”去完成。有了前面“回归”机器学习的思想基础,这个应该很好理解了。
即我会找到大量的“鱼”“猫”和“狗”的图片,每种都对应好标签比如“1”“2”“3”。这时候我们拿这些数据去训练分类器。分类器的训练过程和线性回归基本很相似:
- 建立映射关系的假说即 y=wx+b
- 找到全局损失函数Loss与我们想要求解的w与b的映射关系方程
- 找到Loss符合误差范围的w与b (训练过程结束)
- 拿着训练好的模型去用验证集验证
3.非监督学习–“聚类”
前面我们介绍的线性回归、非线性回归和分类,都属于“监督学习方式”,要在训练数据之前进行标记,这样的数据模型才可以被训练。但数据量很大的时候,人工标注起来是非常困难的。
先回忆一下非监督学习的定义: 获得训练的向量数据后没有标签的情况下,尝试找出其内部蕴含的一种关系的挖掘工作。而聚类,在感性的认知就是把特征形态相同或相近的聚合到一个概念类别下,把特征形态不同的分开。
聚类核心思想:通过对数据进行特征抽象和提取,转换为空间中的向量,通过计算每个“向量”的距离,从远近的角度去判定是否从属一个类别。其本质就是把现实世界中的特征,转化为数学的空间向量,这样我们就把现实的特征问题,转化成了一个可能通过数学方式解决的“向量计算问题”。当然在具体计算的时候还涉及到“特征提取及转换”的步骤(这也是深度学习的重要内容)
举个例子我这里有几个概念,“卡车”、“汽车”、“飞机”和“人”,他们每个都可以用空间中的向量去表示,那么“卡车”与“汽车”的距离就应该是最近的,其次是“飞机”,因为他们都属于“交通工具”这个大类,“汽车”与“人”代表的向量应该是空间中距离最远的,这样就是实现了现实世界概念特征的聚类。
4.机器学习的复盘
到这里已经把机器学习中最重要的概念和原理大体讲了一遍。其实发现并没有特别难的样子,主要在于理解机器学习的思想与基本原理。
其实机器学习(深度学习)都是手段,我们的目的是让计算机可以对现实物理世界比如图像、声音、视频等进行分类、识别甚至一定程度的理解和反馈。可计算机并不能像人类一样可以进行抽象思考,而机器学习的本质,就是把这些物理世界的特征进行数学化,转换成计算机可以听懂的语言,这样它就可以对这些“数学化的物理特征”进行计算了,只不过在我们看来,它好像是通过像人一样学习和思考似的。
对于如何判定机器学习的结果,其本质也是转换成数学中的误差问题进行求解,找到符合我们要求的误差,即认为机器学习完成。
最后我们记住一个公式: y=wx+b,看似简单的公式,后面在神经网络和深度学习中会经常用到,而且无论是学习方式的转换,还是神经网络结构的变换,其最终目的,简单理解的话都可以认为是建立损失函数Loss与w和b的一个映射关系,找到Loss符合我们要求的对应的w和b。(当然怎么找,这就非常复杂了,我也在学习中)
机器学习的部分就分享到这里,下一篇会更新有关“神经元和神经网络”的知识,这是了解深度学习的基石。
既然来了,说些什么?