My Secret Rainbow

告别AI模型黑盒子：可解释的神经网络研究

引言

你是否曾被无理拒绝贷款而烦恼？你是否怀疑过自己的汽车自动驾驶的安全性？你说这种药物能治疗肺癌，为什么呢？种种怀疑充斥在科学研究、金融市场等领域。众所周知，机器学习模型，如神经网络，深度神经网络等，有非常不错的预测能力，但是让人信任一个模型的结果除了有良好的精度之外，可解释性也是一个重要的因素。本文将介绍机器学习模型可解释性的定义、性质和方法，并在后续的文章中，着重介绍不同解释模型的方法，力求在维持模型精度的同时，通过更好的解释模型方法，提高模型的可解释性，从而提高人们对模型和模型结果的信任和接受程度。

一、简介

模型的可解释性目前没有统一的定义，在不同场景中有多种概念，可以揭示不同的理念，展示出科学的特征，它可以帮助我们更深入的了解问题、数据和模型运行。部分机器学习在低风险环境下，错误不会造成严重影响，例如电影的推荐系统，推荐错误造成的影响比较低，这时可解释性的需求也会降低。然而，当机器学习模型应用于其他关键领域时，我们对可解释性便会有更多的需求，如科学领域，需要可解释性对模型进行理解、信任和模型结果的理解，又如在刑事司法制度、金融市场等受监管行业，我们不仅需要人们充分理解这些模型，还需要模型的解释符合法律规范，因此我们要对可解释性进行深入的了解。

二、可解释性的目的

1.信任度

这是一个主观的定义，人们要信任一个模型通常基于两点：一是模型在实际场景有良好表现且不会产生偏见；二是即使模型犯错，也在人们可接受范围。通过模型的可解释性，可以针对以上两点对模型进行描述，使人们对模型产生信任。

2.科学与因果关系

人脑对于不可预料的事情有更新能力，通过这种更新我们可以解释不可预料的事件。例如，一个人突然上火了，他回想起来自己刚吃完荔枝，而他每次吃完荔枝就会上火，此时他就能更新自己的认识，知道吃荔枝会导致我上火，那以后我要少吃一点荔枝。同理，科学研究的结果也需要对这种不可预料或与认知不同的事件进行解释，为什么会有这样的预测或行为呢？我们便需要对结果解释，建立因果关系。此外，研究者通常希望从监督学习模型中推断出一些性质或产生一些假设，而并不是每一个模型都能揭露出这种因果关系。一个可解释模型，如决策树等，可以从观测数据中推断出因果关系，从而给后续的研究带来强有力的线索。同时，当预测或行为是通过大数据和黑盒模型（Black-Box Model）得到的，模型的可解释性还能帮助我们获取额外的模型中的知识。

3. 模型的修复与更新

可解释性可以帮助我们修复和更新模型。例如，在自动驾驶领域中，我们通过深度学习系统识别骑自行车的人。这种识别的准确度要求是非常高的，因为一旦发生错误，后果不堪设想。而可解释性可以帮助分析模型识别的重要特征，例如，模型通过两个轮子识别出了自行车，进一步我们会想到特殊情况，自行车后轮上旁边放两个包也必须要识别出是自行车，从而不断更新深度学习模型（未识别出、识别出 ）。又例如，分类器把一个物品误识别为自行车，根据可解释模型我们可以发现分类错误的原因是自行车道出现在了图片当中，从而修复模型（识别错误、识别正确），将识别重点放在自行车的轮子上。

4.社会可接受度

在默认情况下，机器学习模型可能由于训练数据导致模型存在偏见，如性别歧视、种族歧视等。可解释性便给我们提供了一个监测偏见的工具。在一些模型中，例如美国的再犯预测系统，我们需要说明预测结果并不基于种族来判定，而传统的模型评估（精度、AUC等）是不能说明模型是怎样做决策的，因此我们需要创造或提高模型可解释性，从而展现出模型的公平性，使得模型更被社会大众所接受。

5.可转移性

有时候，我们不仅需要模型在一种情况下可以使用，还需要其应用到其他领域或不熟悉的场景，模型的可解释性便给这种可转移的能力提供了条件。Caruana等人（2015）曾描述过一个模型，该模型应用于预测肺炎导致死亡概率的研究。模型将带有哮喘的病人的死亡风险归类为低风险。实际上，这种低风险是归功于这类病人受到了更激进的治疗。但如果使用该模型帮助分诊，这类病人就会判定为低风险的病人，从而接受保守的治疗，导致病情加重。由于黑盒模型的不可解释性，我们无法发现这种错误，而可解释模型则可以避免这种情况，使模型合理的应用于各种环境当中。

三、可解释性的性质

通过解释方法（算法，模型，可视化等），我们可以产生解释。研究解释方法和解释的性质有助于我们判断解释方法和解释的好坏。

1.解释方法的性质

• 表达能力：解释的方法能够产生有良好的语言或结构的解释的能力，如因果关系等
• 透明度：解释方法在多大程度上依赖于机器学习模型的信息。如解释方法依赖于线性模型（系数），则称该方法有高透明度；依赖于黑盒模型，则透明度较低，因为黑盒模型提供的信息较少；而仅依赖于数据本身的解释方法是零透明度的，因为没有模型信息
• 可移植性：解释方法可应用于的模型的范围。低透明度的解释方法有高可移植性，因为这些方法把模型当作黑盒模型。仅能用于一个模型的解释方法只有低可移植性
• 算法复杂度：解释方法产生解释所需的时间

2.个体解释的性质

• 准确度：解释未知数据的预测的好坏
• 保真度：解释近似于黑盒模型结果的程度，高精度模型的高保真度解释必定是准确的
• 一致性：不同模型产生了相似的结果，对这个结果的解释的差异程度；视具体情况而定，不一定越高越好
• 稳定性：同一模型对相似例子的解释是否也相似
• 可理解性：解释是否被人们所理解
• 正确性：解释是否反映了机器学习模型的正确程度
• 代表性：解释包含的例子是否充分

四、可解释模型介绍

实现可解释性的最简单方法是使用可解释模型。常用的可解释模型包括线性回归，逻辑回归，决策树，RuleFit算法等等，接下来我们将从可解释性方面简单介绍几个模型：

1. 线性回归

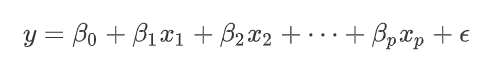
线性回归是最常用的可解释模型之一，通过特征的权重相加可以得到回归的结果。根据特征类型的不同可以对特征的权重进行解释,包括文字解释和可视化解释：

• 文字解释：在其他特征值保持不变的情况下，某个特征

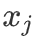
增加一个单位（或：从一类变成另一类），预测值

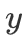
则增加

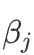
个单位

• 可视化解释：

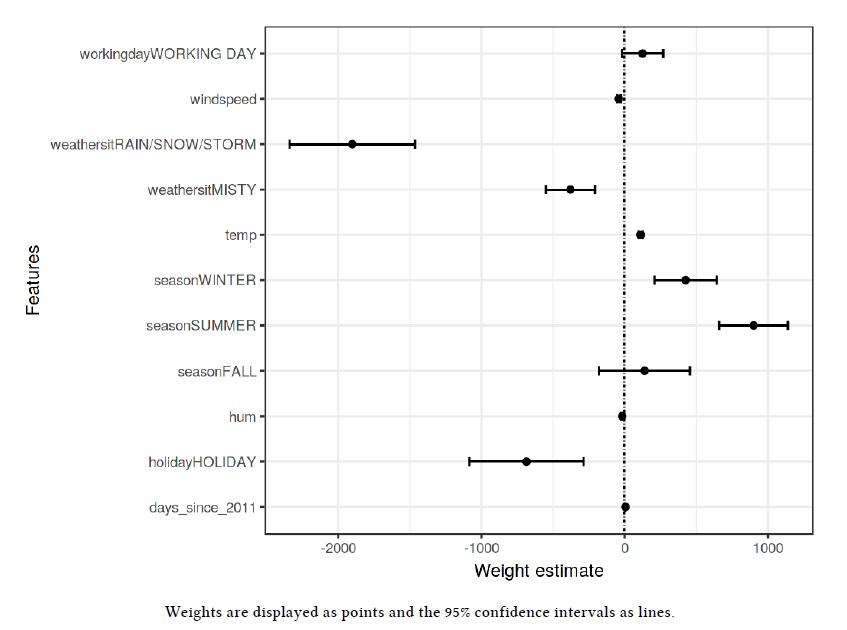
可视化图可以直观的展现出每个特征的权重（实心点）和其95%的置信区间（线段）。

对于单个样本，只需将每个特征的值乘上相应的系数即可得到每个特征的影响。当特征的数目太多（成百上千）时，模型可能会包含很多无关的特征，我们不能将所有的特征的加入到模型当中。为了解决该问题，我们还可以通过L1正则化的方式减少特征的个数，使模型有更好的解释，得到稀疏的线性模型。

线性回归模型的解释可以很好的被人们所理解，这种权重的相加使人们清晰的看到预测是如何得到的，还可以提高模型的可解释性。然而，线性回归模型只能展示线性关系，也忽视了特征之间的交互影响。同时，在解释的时候，我们都有一个前提条件：保持其他特征不变的情况下，这是在实际生活中十分难实现的，特别是当特征之间的相关性较强时，解释就变得很奇怪了。

2. 逻辑回归

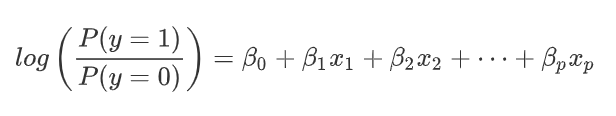
逻辑回归也是常用的可解释模型之一。逻辑一词是logistics [lə’dʒɪstɪks]的音译字,并不是因为这个算法是突出逻辑的特性。上述线性回归模型只能用作回归任务，对于分类任务，线性回归模型是无法处理的，这个时候，逻辑回归就派上用场了。逻辑回归的公式与线性回归的公式有点相似，都是一系列特征权重的相加，不同点在于逻辑回归的结果是一个概率。

上面等式中，我们称log函数里面的部分为几率（odds），是指某事件发生的可能性(概率)与不发生的可能性（概率）之比。根据等式，我们可以得到这样的文字解释：

• 在其他特征值保持不变的情况下，某个特征

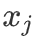
增加一个单位（或：从一类变成另一类）， 几率是原来的

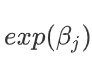
倍；

逻辑回归的优点和缺点比较相似，都是通过权重的相加来解释模型，而交互项，前提条件，也是逻辑回归需要解决的问题。

3. GLM与GAM

在使用线性回归模型时，我们需要很多假设前提，当数据不满足这些假设时，广义线性模型（GLM）与广义加性模型（GAM）就派上用场了。有关注我们公众号的读者必定对这两个模型并不陌生，之前Yvonne曾给大家介绍过《参数模型与非参数模型》，这篇文章非常详细清晰的介绍了GLM和GAM模型，在此我们也不赘述，我们将从模型的可解释性方面进行探讨。

当模型的输出不符合高斯分布时，GLM模型作为线性回归模型的拓展，能继续使用特征权重的相加来拟合模型，这就在保留了线性回归模型的可解释性的同时，为其他分布的输出数据的解释提供了可能性。逻辑回归便是GLM模型的一种。

GAM模型则解决了模型特征与输出的非线性关系。GAM模型的核心仍然是特征影响的和，只不过这个和不仅仅可以表示线性关系，还能表示非线性关系，这种非线性关系可以通过机器学习算法学习得到。

GLM和GAM模型已经被使用了很多年，在科学领域中模型已经被反复研究，得到了研究者的信任。在提供了可解释性的同时，这两种拓展为更多数据类型提供了研究方法。当然，这两种模型在可解释性方面也有不足。GLM模型对于复杂分布的数据会更加难以解释（根据连接函数的复杂性），GAM模型也会由于特征与输出的非线性关系使得解释不够直观，更加复杂。因此这两个模型的可解释性会比线性回归模型稍差一点。4.决策树根据任务的不同，回归任务我们选择线性回归模型，分类任务我们选择逻辑回归模型，而在非线性和交互项的情况下，这两种模型的使用就会受到挑战，此时，决策树模型的出现便解决了这些问题。决策树既能完成分类任务，也能完成回归任务。决策树模型呈树形结构，从根结点（顶部）开始，对实例的某一特征进行测试，根据测试结果，将实例分配到其子结点；这时，每一个子结点对应着该特征的一个取值。如此递归地对实例进行测试并分配，直至达到叶结点（底部），最后将实例分到叶结点的类中。

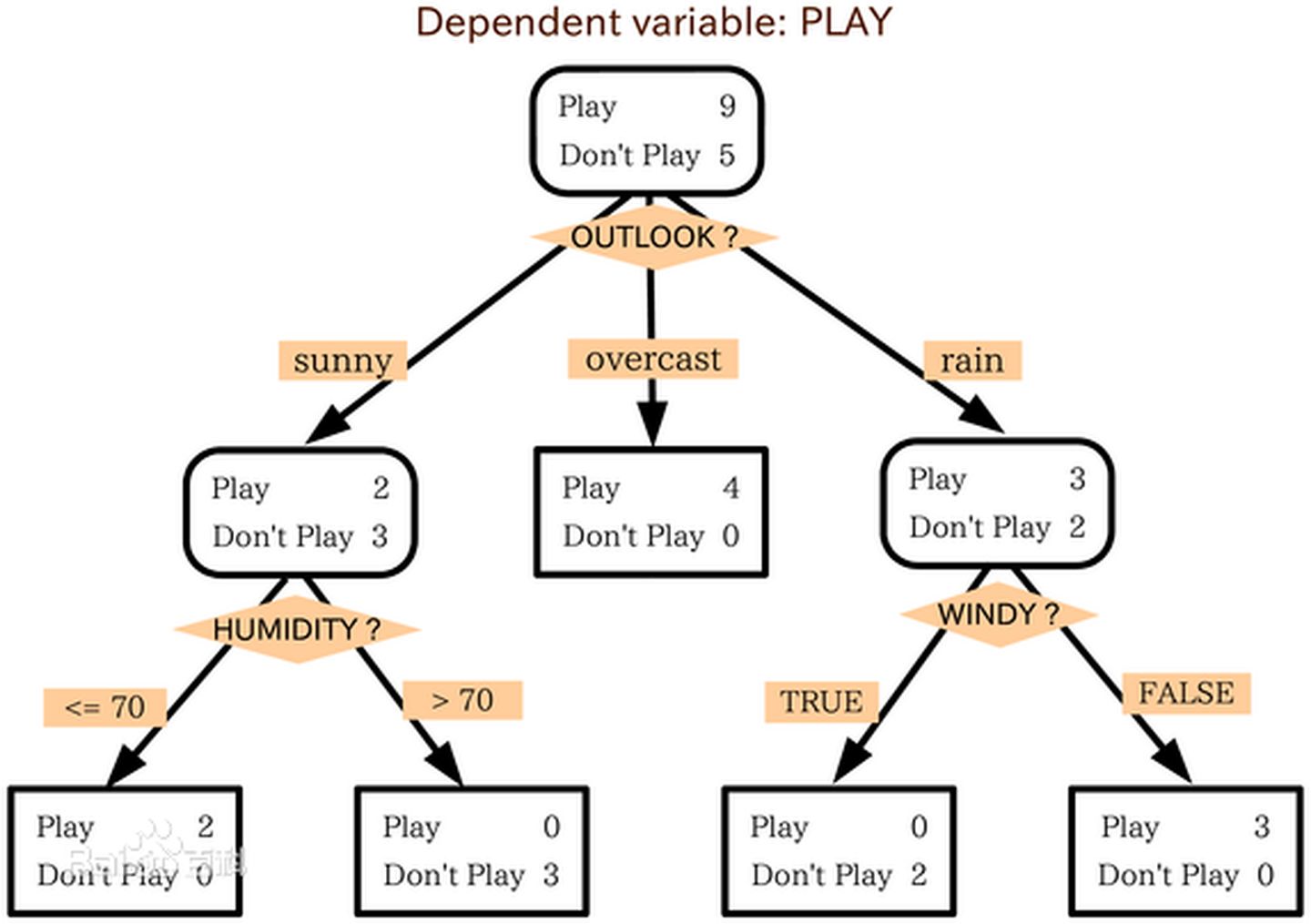
决策树算法也有很多，包括ID3、C4.5与CART等，算法的介绍大家可以阅读李航的《统计学习方法》等书籍，接下来我们将根据CART算法介绍决策树的可解释性（其他决策树算法的可解释性也类似）。

决策树的解释比较简单，从根节点开始，根据判断条件走到下一个子结点，一直到叶结点便是对应的预测结果，利用IF-THEN规则，将“路径”上的各判断条件用“和”连接起来，如上图的解释：

• 如果天气是晴天，且湿度小于等于70，那么便出门玩耍从根结点到叶结点，树型结构给予了单个预测直观的解释；从叶结点到根节点，我们可以根据自己想要的预测值，找到实现预测的特征。

我们还可以根据平方误差最小化准则或基尼指数（Gini index）最小化准则，计算每个特征的重要性，特征重要性的总和为100，如下面例子：

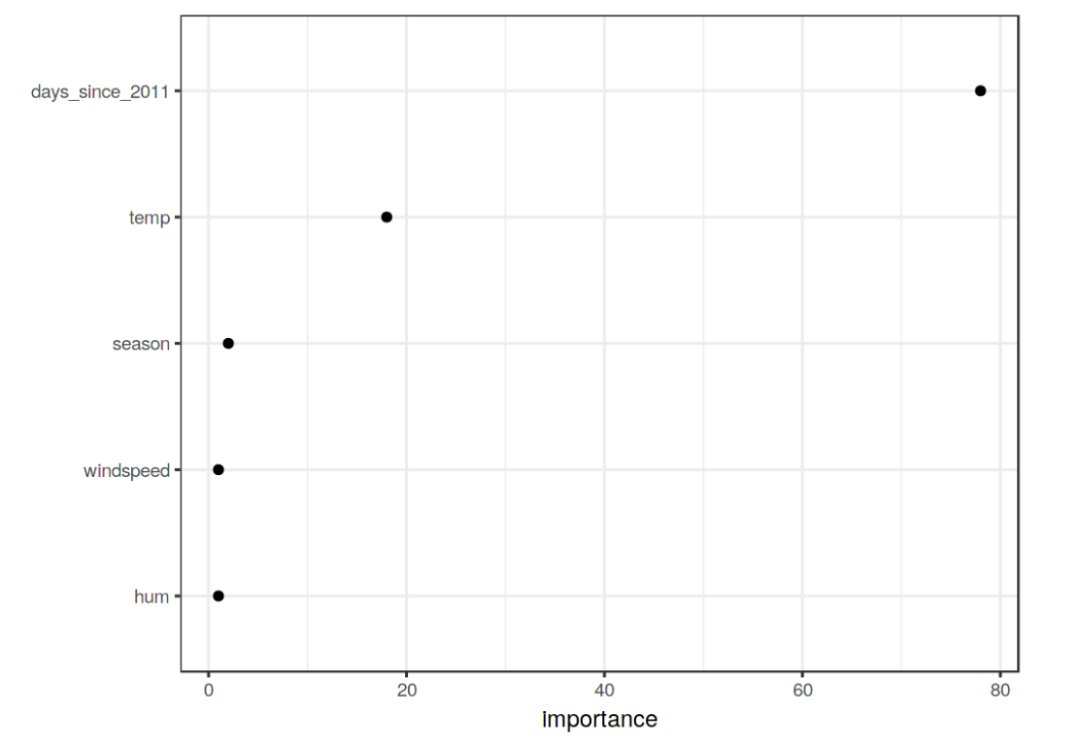
特征重要性展示了一个特征对提升结点纯度的程度。上述例子表明，时间特征更加重要。

我们可以看到，决策树模型除了文字解释外，可以通过可视化展现出各个结点的关系，使得解释更加直观，更容易被理解。决策树模型还包含了交互项因素，不像线性模型还需要考虑是否要添加交互项；线性模型有时候还需要对特征进行变换（如取log），决策树则免除了这一操作。和之前几个模型一样，决策树模型在解释上也有自己的缺点：首先它无法表示线性关系，由于每个结点都是作为一个判断，最终的结果只能表达为一个阶梯函数；进一步，一个细微的特征变化会导致判断的改变，对结果有很大影响，如上述决策树图，湿度在69.99和70.01是完全不同的结果，这种解释是不能被接受的。其次，决策性树的不稳定性也给它的解释性带来了挑战。训练集的变化会完全改变决策树模型，根结点的选择不同，整个树结构就会完全不同，这种不稳定性使得解释不被轻易信任。最后，叶结点越多，层次越深，也会使得解释更复杂，让人更难理解，控制好叶结点数和特征数目可以更好的提高决策树的可解释性。

5. RuleFit算法

RuleFit算法由Friedman和Popescu在2008年时提出，它巧妙的将决策树和线性模型结合在一起，以此解决线性回归模型的交互项问题。从字面意思理解， “RuleFit” 就是将规则拟合的意思。决策树的“路径”便是一种规则，它是特征决策的组合，如上文的“晴天且湿度小于等于70度”就是一条规则，这种规则包含了特征之间交互项的影响。算法分为两步：首先通过决策树模型产生规则，再将原有特征（最终也称为规则）和这些新产生的规则作线性组合，拟合出一个稀疏的线性模型（LASSO）。由于这个算法得到的是稀疏线性模型，且规则由决策树产生，因此模型的可解释性得以大大保留。

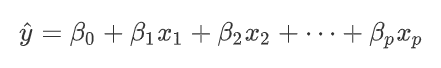
这里的

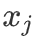
既能是原有的特征，也可以是新产生的规则。

在解释方面，原有特征作为线性部分与线性回归模型的解释相同，新产生的规则则可以看作一个二分类特征，1表示完全符合规则，反之，取0。同时我们还能计算出各个规则的重要性，包括了原始特征的重要性和所有规则的重要性。我们可以看看以下例子：

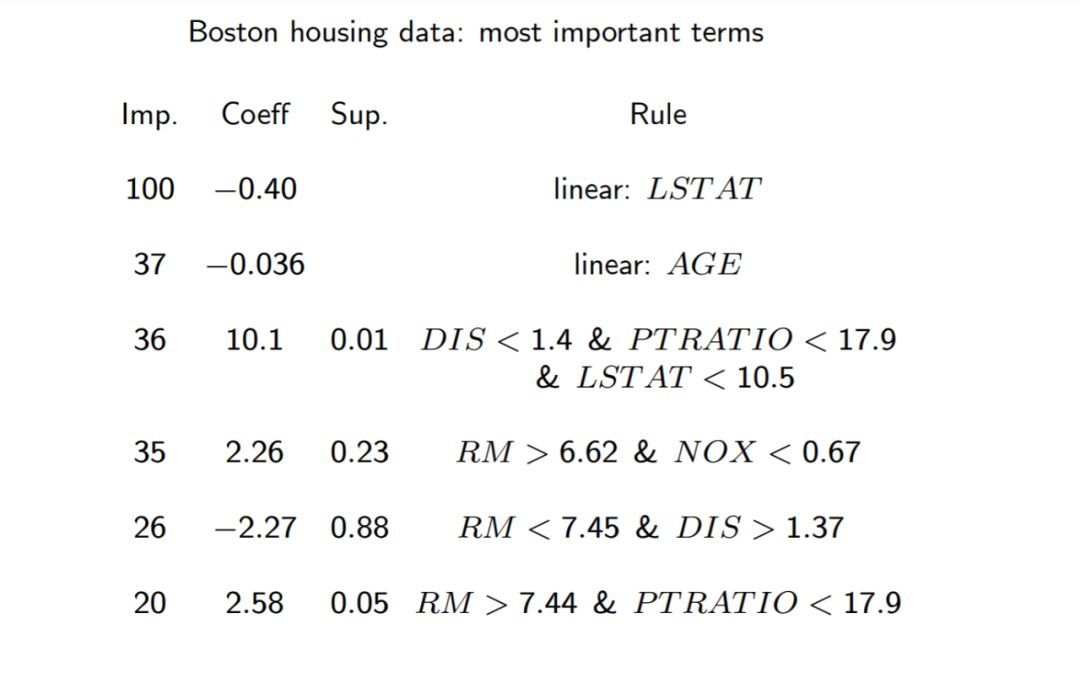
我们可以看到规则中，有原有的特征（LSTAT、AGE），也有由决策树产生的规则，其中LSTAT这个特征的重要性最高（Imp）。对于新产生的规则的解释，我们仍然用IF-THEN的方法，如第五条：在其他条件保持不变的前提下，如果房间数目（RM）少于7.45且距离工作中心（DIS）大于1.37英里，房子的价格将减少2.27百万（Coeff）。

RuleFit算法很好的解决了线性模型中可能需要手动添加交互项的问题，同时在产生的规则不复杂（最多3个特征结合）的情况下，得到的模型的可解释性较高。而稀疏线性模型包含的规则（特征）不多，因此模型的局部可解释性（单个例子的解释）也得到了提升。而模型的不足之处在于，模型的规则依赖于决策树（或随机森林）的表现，一旦结果不好会进一步降低整个模型的准确率，进而降低了模型的可解释性。同时，由于线性模型解释的前提：保持其他条件不变，当规则出现重叠时，解释也会变得奇怪。例如：一条规则是房间数目少于6，另一条规则是房间数目少于7.45且距离工作中心大于1.37英里，当我们解释第二条规则的系数时，保持其他规则不变是不可能的，这样系数的解释就变得复杂多了。

五、与模型无关的解释方法

通常，通过ROC曲线、MSE、MAE等评价标准，我们对模型的查全率、查准率、精确度等有直观的认识，这些标准可以用来评价所有的监督学习模型，但无法展示模型的可解释性，因此我们需要找到模型通用的解释方法。

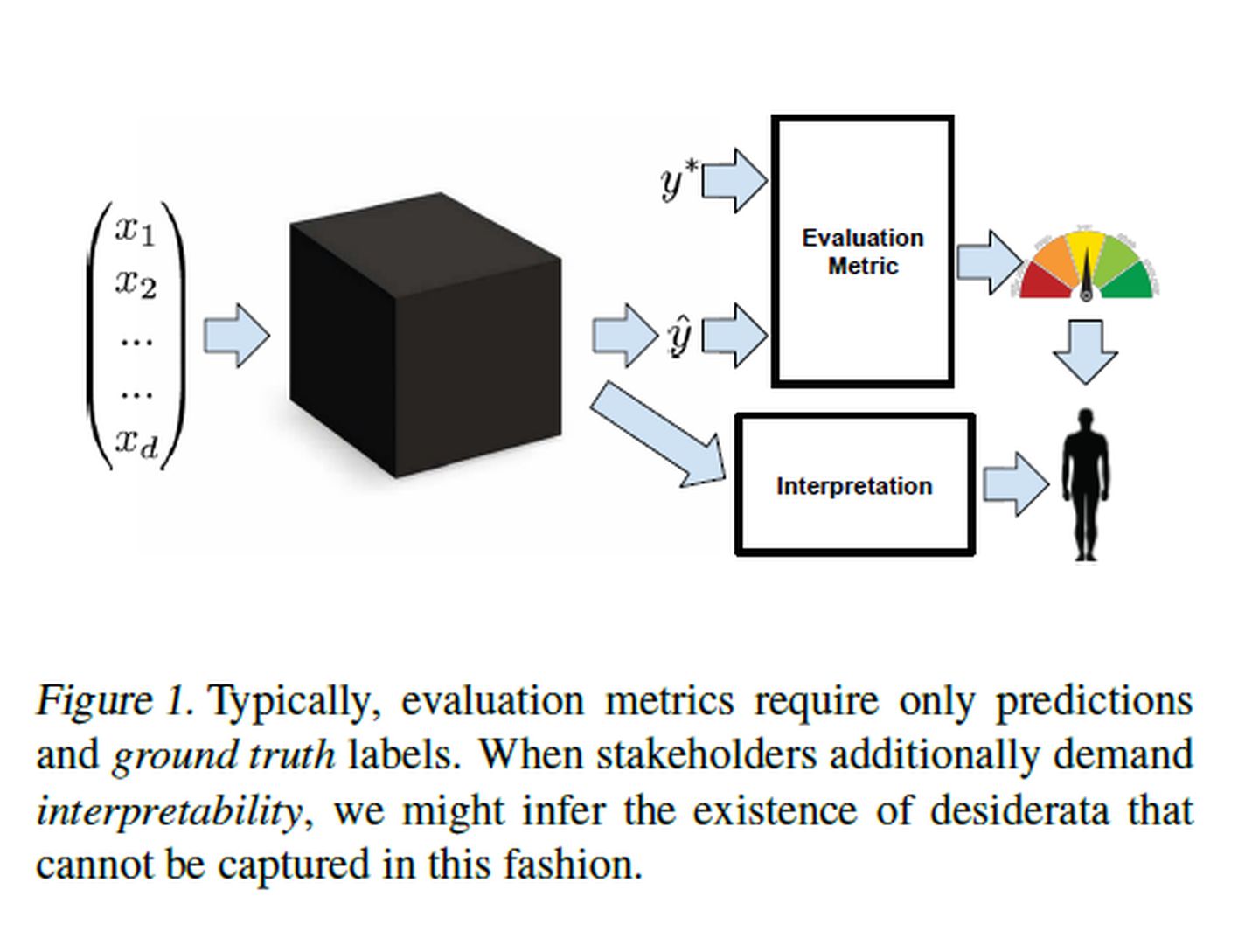
Ribeiro等人（2016）提出了与模型无关的解释方法，这种解释方法是将解释从机器学习模型中分离出来，它最大的好处是其灵活性。它能用于各种机器学习模型，能用不同的表达方法展示可解释性，使黑盒模型更加透明。目前，这种可解释方法包括PDP（Partial Dependence Plot），ALE图（Accumulated Local Effects），特征交互性图，特征重要性图，LIME算法等等。我们先对这些方法有个基本认识，在下几期文章中，再对每个方法进一步深入探究，有兴趣的读者们可以通过订阅我们的公众号，关注可解释领域的研究。

1. 部分依赖图（PDP）

PDP是用来解释某个特征与输出的关系，是一个全局解释方法。PDP是依赖于模型本身的，所以我们需要先训练模型。假设我们想知道某特征和研究输出的关系，利用边缘分布，可以得到关于该特征和输出的函数关系。通过画图，可以分析该特征与预测是线性的还是单调的还是其他类型的，图像都一目了然。

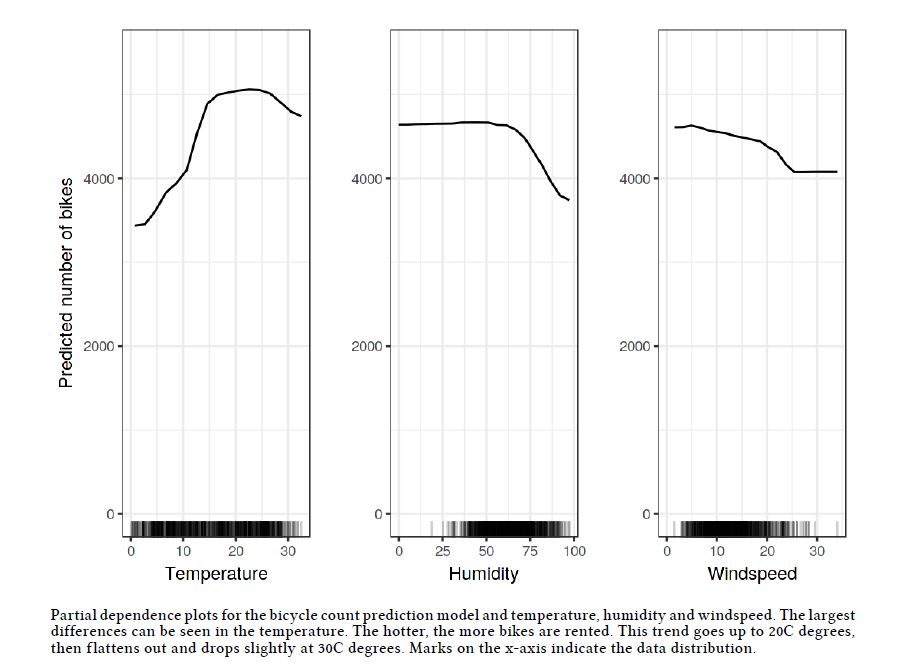
如上图，我们可以直观的看到每个特征与预测值的关系，纵坐标表示在某个特定特征值位置时预测的平均值。但PDP也有很大的局限性，每个特征必须符合独立假设，否则得到的解释也许是错误的。

2. ALE图

使用PDP的假设条件是独立性，它假设计算的特征和其它特征是不相关的。当特征是相关的时候，PDP不再有说服力。对这个问题的一个解决方法就是ALE图（Accumulated Local Effects），它工作在条件分布下而不是边缘分布下。ALE巧妙的将有相关的特征的影响独立出来，根据条件分布，得到在特定特征值时，预测值在局部范围内的平均变化。

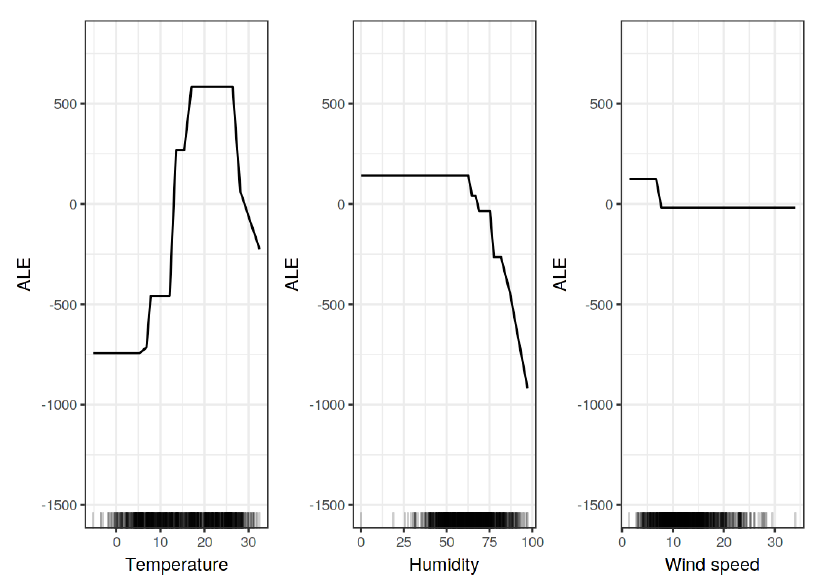
与上图的PDP作为对比，ALE在高温或高湿度情况下下降更快。原因是ALE计算的是单个特征的影响，PDP在计算时包含了该特征与其他特征的相关性。ALE图同样可以直观的看到每个特征与预测值的关系，并且在特征变量有相关性时仍能使用，计算速度也比PDP快。当然，ALE图也有很多需要优化的地方，但与PDP相比，ALE仍是解释模型时首选的可视化方法。

3. 特征交互项与特征重要性

针对黑盒模型，输入特征与输出的关系是模糊的。通常我们需要知道以下问题：哪个特征对结果产生的影响更大？特征是怎样影响结果的？是否存在交互项？假如存在交互项，预测便不能简单的表达成一系列特征影响的和，因为特征的影响会随着其依赖的特征的值而变化。特征交互作用强度图可以用于判断交互项存在的可能性，特征重要性图则可以看到每个特征的重要性。

3.1 特征交互项作用强度图

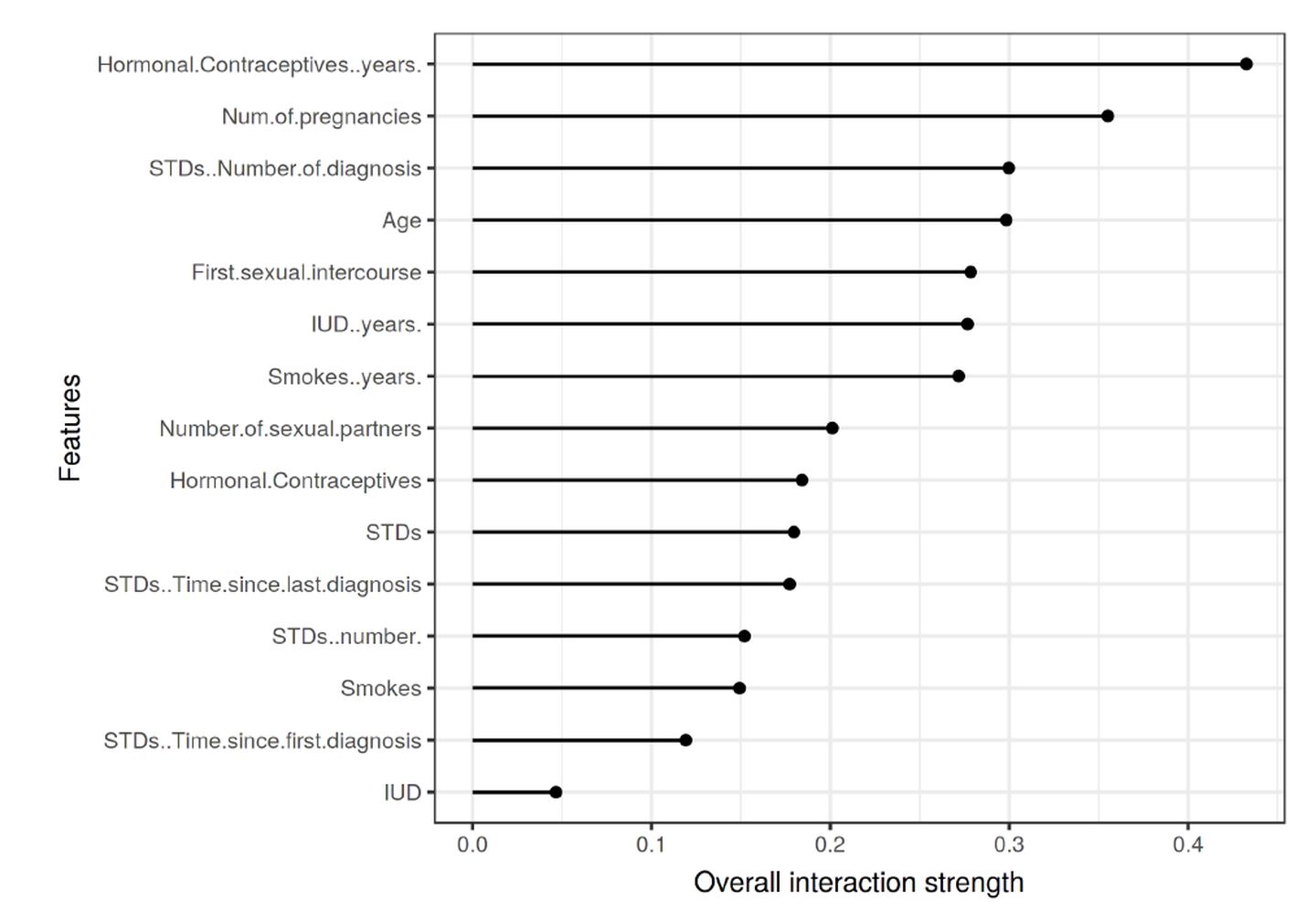
该图横坐标是特征的总体交互项强度，纵坐标是特征名称。例如，我们看到激素避孕时间和怀孕人数这个两个特征，可能与其他特征存在交互作用。再进一步，我们研究怀孕人数和其他特征的两两交互情况：

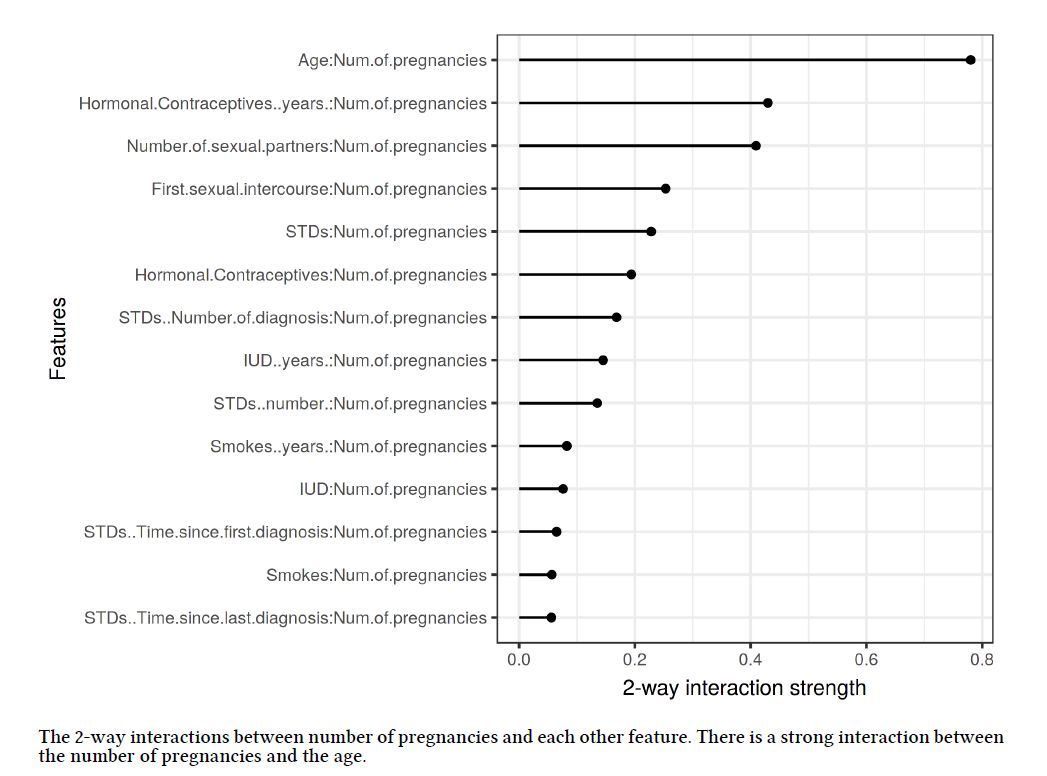
从上图可以看出，年龄和怀孕人数有很强的交互作用。

3.2 特征重要性图

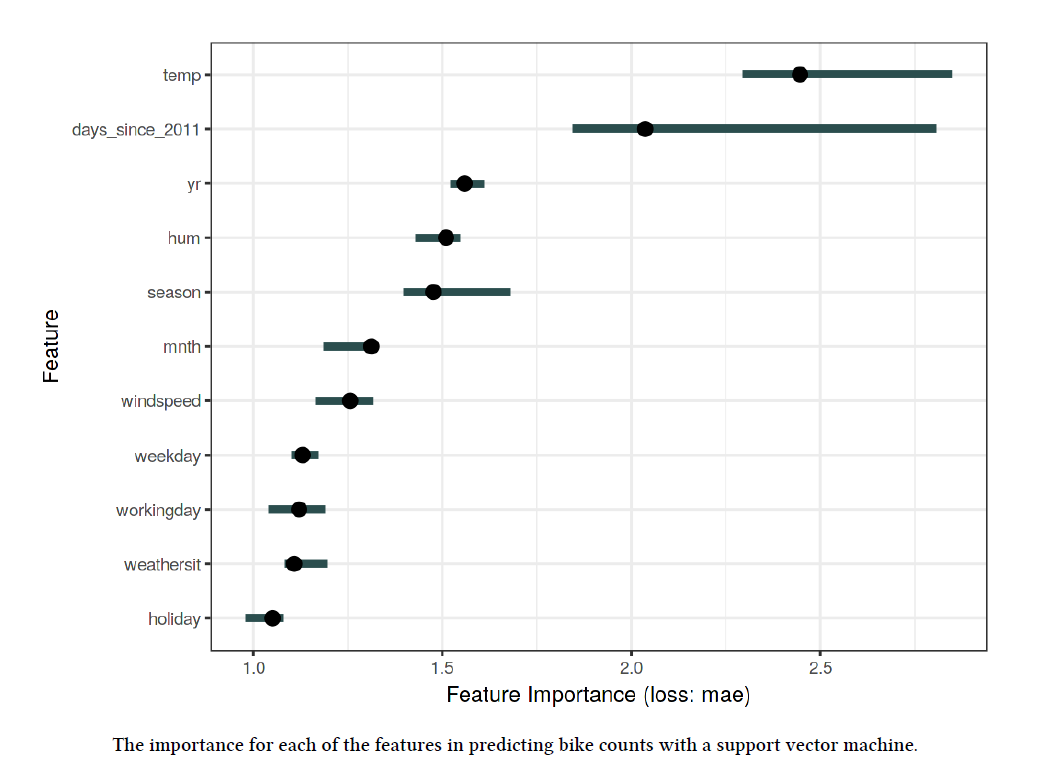
该图横坐标是特征的重要性，误差衡量标准是MAE，纵坐标是特征名称。由上图可以看到，温度因素在这个模型中是最影响预测结果的。这两类图像的解释在全局上都能很直观和清晰的表现出特征与结果的关系，但在计算强度值和重要性时都存在一定的缺点，目前的在这方面也有不少的研究，后续文章我们将继续介绍。

4. 局部可解释性描述（Local Interpretable Model-agnostic Explanation，LIME）

LIME是围绕单个样本建立局部代理模型的一种方法。LIME通过训练一个可解释模型去替代黑盒模型，LIME的实现可以遵循如下流程：

• 选择想要解释某个例子的预测结果；
• 打乱数据集，产生新的样本（或随机生成新的样本）。如：“我爱索信达”，提取“我信”作为新的样本；
• 用黑盒模型训练新的样本，得到相应的预测结果；
• 计算新的样本与想要解释的例子的“距离”，得到每个新的样本的权重，“距离”越近，权重越高；
• 以加权后的新样本作为自变量，做L1正则化线性回归模型，这个线性模型的参数可以是用来解释预测结果是如何得到的。

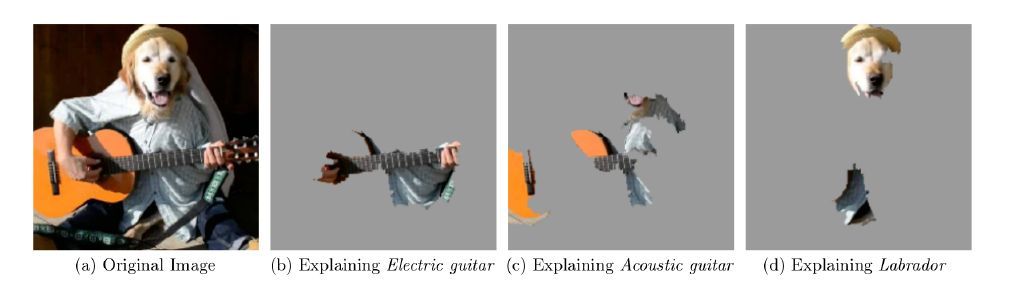
LIME模型能够表示出模型预测结果的原因，如上图，（b）（c）（d）分别解释了为什么图片会识别为电吉他、木吉他、拉布拉多犬，增强我们对黑盒模型结果的信任；同时，LIME模型能够发现重要变量对模型预测结果的影响，当数据存在扰动时，通过LIME检测模型的稳定性。

六、展望

现有的模型和解释方法给可解释性提供了大量的条件，现实生活的例子和机器学习结果的差异使得机器学习在可解释性方面还有大量值得研究的地方。未来模型的可解释性将专注于上与模型无关的解释方法，提高解释精度，拓展解释范围，增加可解释的自动化（如：自动计算特征重要性）是研究的方向。以前的统计分析数据需要符合很多假设条件，如正态性，独立性等，现在机器学习模型避免了这些假设条件后，推动了研究内容从数据向模型转变。可解释性将机器学习以更有效、更透明的方式传达给研究者，实践到更多的研究中，我们也将在后续给各位读者详细介绍更多、更详细的可解释方法，一起走进可解释的世界。

参考资料

[1] Christoph Molnar. Interpretable Machine Learning[2]Zachary C. Lipton . The Mythos of Model Interpretability[3]36大数据（http://36dsj.com)：36大数据» 关于如何解释机器学习的一些方法[4]Friedman, Jerome H, and Bogdan E Popescu. 2008. “Predictive Learning via Rule Ensembles.” The Annals of Applied Statistics. JSTOR, 916–54.[5]Ribeiro, M.T., Singh, S. and Guestrin, C., 2016, August. Why should i trust you?: Explaining the predictions of any classifier. In Proceedings of the 22nd ACM SIGKDD International Conference on Knowledge Discovery and Data Mining (pp. 1135-1144). ACM.

 

原文：https://zhuanlan.zhihu.com/p/86728091